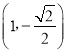Question

【题目】已知函数，且x＝0是f（x）的极值点.

（1）求f（x）的最小值；

（2）是否存在实数b，使得关于x的不等式ex＜bx+f（x）在（0，+∞）上恒成立？若存在，求出b的取值范围；若不存在，说明理由.

Answer 1

【答案】（1）1（2）存在；b的范围为[1，+∞）

【解析】

（1）由已知结合极值存在条件可求m，然后结合导数单调性及最值的关系即可求解；

（2）由已知不等式代入整理可得，可考虑构造函数，结合导数与单调性的关系对b进行分类讨论可求.

解：（1），

由x＝0是f（x）的极值点可得10，即m＝1，经检验m＝1符合题意，

，

设g（x）＝ex（x+1）﹣1，则g′（x）＝ex（x+2）＞0在x＞﹣1时恒成立，

故g（x）在（﹣1，+∞）上单调递增且g（0）＝0，

所以，当x＞0时，g（x）＞0即f′（x）＞0，函数f（x）单调递增，

当﹣1＜x＜0时，g（x）＜0即f′（x）＜0，函数f（x）单调递减，

故当x＝0时，f（x）取得最小值f（0）＝1；

（2）由ex＜bx+f（x）在（0，+∞）上恒成立可得，

设，则需要，

又，

（i）若b≥1，则x＞0时，0，h（x）单调递减，

所以h（x）＜h（0）＝0，符合题意，

（ii）若b≤0，则x＞0时，0，h（x）单调递增，h（x）＞h（0）＝0，不符合题意，

（iii）若0＜b＜1，令，得x，

当x时，h′（x）＞0，h（x）单调递增，此时h（x）＞h（0）＝0，不满足题意，

综上，b的范围[1，+∞）.