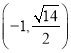Question

【题目】已知椭圆：过点，、分别为椭圆C的左、右焦点且

（1）求椭圆C的方程；

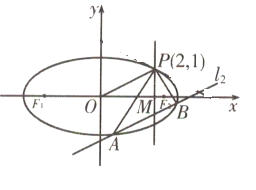
（2）直线平行于OP（O为原点），且与椭圆C交于两点A、B，与直线x＝2交于点M（M介于A、B两点之间）．

（I）当△PAB面积最大时，求的方程；

（II）求证：.

Answer 1

【答案】（1）1；（2）（I）；（II）证明见解析.

【解析】

（1）由可得c的值，又椭圆过定点P可得a，b的关系，再由a，b，c的关系求出a，b的值，进而求出椭圆的C的方程；

（2）（I）求出OP的斜率，设直线的方程，然后与椭圆方程联立，求出弦长AB，再求P到直线的距离，代入面积公式，由函数的单调性求出面积最大时的直线的方程；

（II）计算出直线PA，PB的斜率之和为0，可得PM为∠APB的角平分线，由角平分线的性质可证．

（1）因为，，

所以

所以，

由于椭圆过点，所以，，解得：，

所以椭圆的方程为：1；

（2）（I）因为

所以可设直线的方程为，设，，

联立直线与椭圆的方程，整理可得，

，即，

，，

所以弦长，

P到直线AB的距离为：，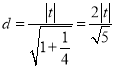

所以，

当且仅当取等号，由M介于A、B之间可得

这时直线的方程为；

（II），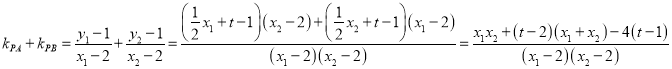

将，，，代入可得，

所以直线PA，PB关于直线x＝2对称，即PM为∠APB的角平分线，

由角平分线的性质可得，

即证得：