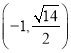题目内容
【题目】已知口袋里装有4个大小相同的小球，其中两个标有数字1，两个标有数字2．
（1）从口袋里任意取一球，求取到标有数字2的球的概率；
（2）第一次从口袋里任意取一球，放回口袋里后第二次再任意取一球，记第一次与第二次取到小球上的数字之和为
．当为何值时，其发生的概率最大？说明理由．
【答案】（1）
；（2）数字和为3时概率最大，理由详见解析．
【解析】
（1）利用古典概型的概率计算公式即可求解.
（2）设标号为1的球为
，
，标号为2的球为
，
，采用列举法求出所有基本事件个数，然后分别求出数字和为2、3、4的基本事件个数，利用古典概型的概率计算公式求出各自的概率即可求解.
解：（1）4个球中标有数字2的球有2个，故所求概率为
，
（2）设标号为1的球为，，标号为2的球为，．
所有基本事件包括：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共16种．
设事件
表示数字和为2，
包括：，，，，共4种，
故有
．
设事件
表示数字和为3，
包括：，，，，，
，，，共8种，
．
设事件
表示数字和为4，
包括：，，，，共4种，
故
．
数字和为3时概率最大．
科学实验活动册系列答案
【题目】2019年春节前后，中国爆发新型冠状病毒（SARS-Cov-2）如图所示为1月24日至2月16日中国内地（除湖北以外的）感染新型冠状病毒新增人数的折线图，为了预测分析数据的变化规律，建立了
与时间变量
的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据（时间变量的值依次为1，2，3，4，5，6，7，8，9，10，11）建立模型①：
；根据2月4日至2月16日的数据（时间变量的值依次为12，13，14，15，16，17，18，19，20，21，22，23，24）建立模型②：
.
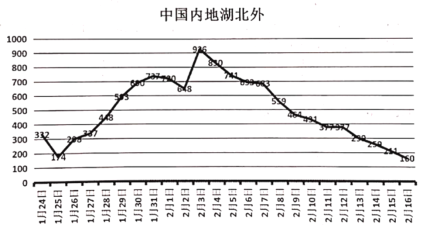
1月 24日 | 1月 25日 | 1月 26日 | 1月 27日 | 1月 28日 | 1月 29日 | 1月 30日 | 1月 31日 | 2月 1日 | 2月 2日 | 2月 3日 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
332 | 174 | 298 | 337 | 448 | 593 | 690 | 737 | 720 | 648 | 926 |
2月 4日 | 2月 5日 | 2月 6日 | 2月 7日 | 2月 8日 | 2月 9日 | 2月 10日 | 2月 11日 | 2月 12日 | 2月 13日 | 2月 14日 | 2月 15日 | 2月 16日 |
12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
830 | 741 | 693 | 683 | 559 | 464 | 431 | 377 | 377 | 299 | 259 | 211 | 160 |
（1）求出两个回归直线方程；（计算结果取整数）
（2）中国政府为了人民的生命安全，听取专家意见，了解了病毒信息，并迅速做出一系列的隔离防护措施，但新冠状病毒在世界范围内爆发时，某些欧美国家采取放任的态度，不治疗、不隔离、不检测，甚至不公布，请你用以上数据说明采取一系列措施的必要性，不采取措施的后果.
参考数据：
，
，
，
参考公式：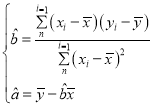
.
