题目内容
设数列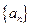 的前
的前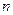 项和为
项和为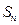 ,已知
,已知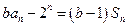 .
.
(1)证明:当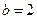 时,
时,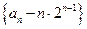 是等比数列;
是等比数列;
(2)求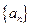 的通项公式.
的通项公式.
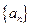 的前
的前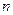 项和为
项和为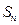 ,已知
,已知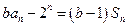 .
.(1)证明:当
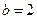 时,
时,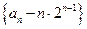 是等比数列;
是等比数列;(2)求
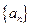 的通项公式.
的通项公式.(1)见解析(2)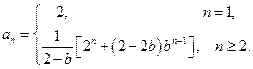
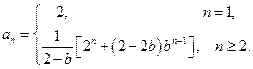
由题意知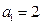 ,且
,且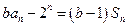 ,
,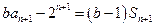
两式相减得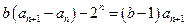 ,即
,即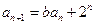 . ①
. ①
(1)当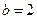 时,由①知
时,由①知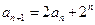 ,
,
于是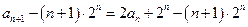
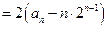 ,
,
又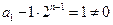 ,所以
,所以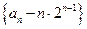 是首项为1,公比为2的等比数列.
是首项为1,公比为2的等比数列.
(2)当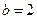 时,由(Ⅰ)知
时,由(Ⅰ)知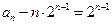 ,即
,即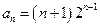 .
.
当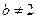 时,由①得
时,由①得
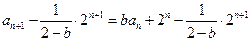
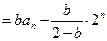
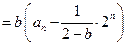 .
.
因此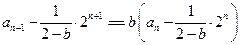
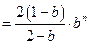 ,
,
得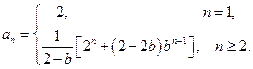
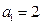 ,且
,且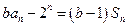 ,
,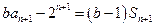
两式相减得
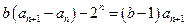 ,即
,即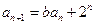 . ①
. ①(1)当
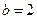 时,由①知
时,由①知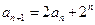 ,
,于是
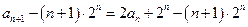
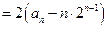 ,
,又
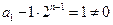 ,所以
,所以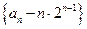 是首项为1,公比为2的等比数列.
是首项为1,公比为2的等比数列.(2)当
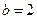 时,由(Ⅰ)知
时,由(Ⅰ)知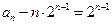 ,即
,即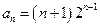 .
.当
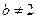 时,由①得
时,由①得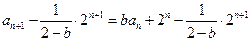
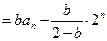
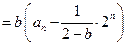 .
.因此
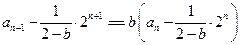
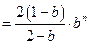 ,
,得
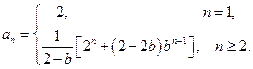

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 }的各项为不等于1的正数,数列{
}的各项为不等于1的正数,数列{ }的通项公式为
}的通项公式为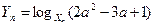 ,其中1<a<
,其中1<a<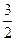 为常数,对于k 、t∈N,k≠t ,满足
为常数,对于k 、t∈N,k≠t ,满足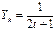 ,
,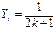 ,是否存在自然数
,是否存在自然数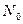 使得n>
使得n>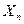 >1恒成立?若存在求出相应的
>1恒成立?若存在求出相应的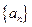 ,公比为
,公比为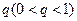 ,
,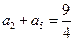 ,
,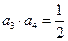 。
。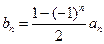 ,求证:
,求证: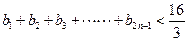 。
。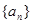 中,
中,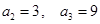 ,若
,若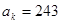 ,则
,则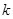 等于
等于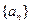 的前
的前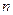 项和为
项和为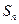 ,已知
,已知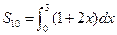 ,
,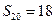 ,
,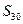 = .
= .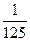 的最小整数n是 ( )
的最小整数n是 ( )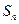 为其前n项和。已知a2a4="1,"
为其前n项和。已知a2a4="1," 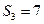 ,则
,则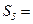



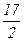
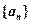 满足:
满足: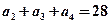 ,且
,且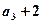 是
是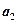 ,
,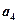 的等差中项,则数列
的等差中项,则数列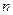 项和
项和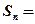 .
.