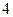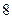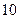题目内容
已知等比数列{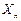 }的各项为不等于1的正数,数列{
}的各项为不等于1的正数,数列{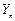 }的通项公式为
}的通项公式为
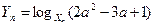 ,其中1<a<
,其中1<a<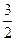 为常数,对于k 、t∈N,k≠t ,满足
为常数,对于k 、t∈N,k≠t ,满足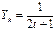 ,
,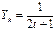 ,
,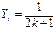 ,是否存在自然数
,是否存在自然数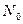 使得n>
使得n>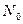 时,
时,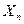 >1恒成立?若存在求出相应的
>1恒成立?若存在求出相应的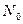 ,若不存在,请说明理由。
,若不存在,请说明理由。
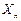 }的各项为不等于1的正数,数列{
}的各项为不等于1的正数,数列{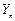 }的通项公式为
}的通项公式为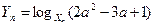 ,其中1<a<
,其中1<a<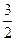 为常数,对于k 、t∈N,k≠t ,满足
为常数,对于k 、t∈N,k≠t ,满足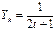 ,
,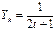 ,
,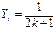 ,是否存在自然数
,是否存在自然数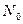 使得n>
使得n>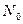 时,
时,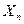 >1恒成立?若存在求出相应的
>1恒成立?若存在求出相应的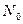 ,若不存在,请说明理由。
,若不存在,请说明理由。见解析
当1<a<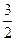 时,
时,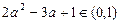 设等比数列{
设等比数列{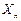 }的公比为
}的公比为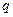 (
(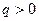 且
且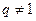 ),由
),由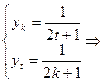
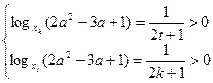 ,
,
由于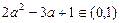 ,
,
得: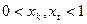 ,∴
,∴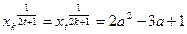 ,
,
即: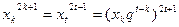 ,化得:
,化得: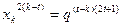 ,
,
不妨设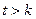 ,∴
,∴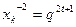 ,
,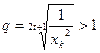 ,
,
而当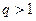 时,对于正项等比数列{
时,对于正项等比数列{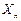 }来说,一定存在自然数
}来说,一定存在自然数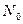 使得n>
使得n>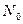 时,
时,
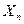 >1恒成立。令
>1恒成立。令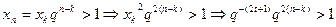
∴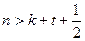 ,令
,令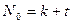 ,则有当n>
,则有当n>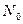 时,
时,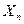 >1恒成立。
>1恒成立。
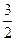 时,
时,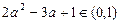 设等比数列{
设等比数列{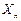 }的公比为
}的公比为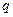 (
(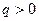 且
且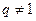 ),由
),由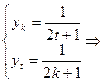
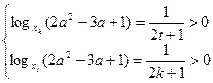 ,
,由于
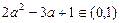 ,
,得:
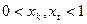 ,∴
,∴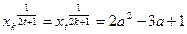 ,
,即:
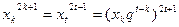 ,化得:
,化得: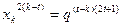 ,
,不妨设
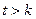 ,∴
,∴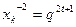 ,
,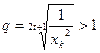 ,
,而当
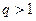 时,对于正项等比数列{
时,对于正项等比数列{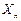 }来说,一定存在自然数
}来说,一定存在自然数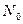 使得n>
使得n>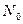 时,
时,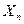 >1恒成立。令
>1恒成立。令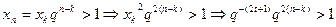
∴
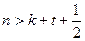 ,令
,令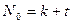 ,则有当n>
,则有当n>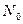 时,
时,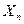 >1恒成立。
>1恒成立。
练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
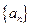 的前
的前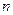 项和为
项和为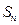 ,已知
,已知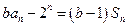 .
.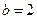 时,
时,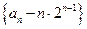 是等比数列;
是等比数列;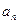 }为等比数列,
}为等比数列,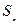 是它的前n项和.若
是它的前n项和.若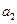 *
*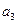 =2a1,且
=2a1,且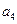 与2
与2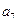 的等差中项为
的等差中项为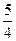 ,则
,则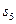 =
=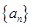 的各项均为正数,前四项之积等于64,那么
的各项均为正数,前四项之积等于64,那么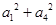 的最小值等于 。
的最小值等于 。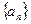 前
前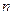 项之和为
项之和为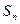 ,
, 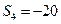 ,
,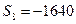 ,求
,求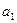 和
和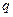
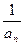 };(6){an+3}中,等比数列的个数是( )
};(6){an+3}中,等比数列的个数是( ) 成等比数列,则
成等比数列,则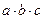 的值为_____________
的值为_____________ 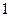 ,项数是偶数,所有的奇数项之和为
,项数是偶数,所有的奇数项之和为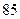 ,所有的偶数项之和为
,所有的偶数项之和为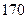 ,
,