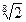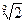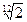题目内容
已知数列{an}满足3an+1+an=4(n≥1),且a1=9,其前n项之和为Sn。则满足不等式|Sn-n-6|<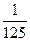 的最小整数n是 ( )
的最小整数n是 ( )
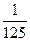 的最小整数n是 ( )
的最小整数n是 ( )| A.5 | B.6 | C.7 | D.8 |
 C
C由递推式得:3(an+1-1)=-(an-1),则{an-1}是以8为首项,公比为-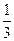 的等比数列,
的等比数列,
∴Sn-n=(a1-1)+(a2-1)+…+(an-1)=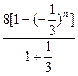 =6-6×(-
=6-6×(-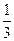 )n,∴|Sn-n-6|=6×(
)n,∴|Sn-n-6|=6×(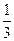 )n<
)n<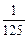 ,得:3n-1>250,∴满足条件的最小整数n=7,故选C。
,得:3n-1>250,∴满足条件的最小整数n=7,故选C。
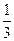 的等比数列,
的等比数列, ∴Sn-n=(a1-1)+(a2-1)+…+(an-1)=
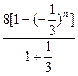 =6-6×(-
=6-6×(-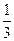 )n,∴|Sn-n-6|=6×(
)n,∴|Sn-n-6|=6×(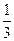 )n<
)n<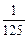 ,得:3n-1>250,∴满足条件的最小整数n=7,故选C。
,得:3n-1>250,∴满足条件的最小整数n=7,故选C。
练习册系列答案
相关题目
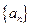 的前
的前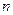 项和为
项和为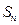 ,已知
,已知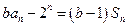 .
.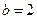 时,
时,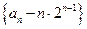 是等比数列;
是等比数列;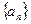 前
前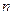 项之和为
项之和为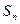 ,
, 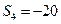 ,
,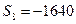 ,求
,求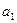 和
和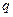
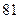
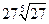
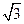
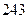
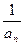 };(6){an+3}中,等比数列的个数是( )
};(6){an+3}中,等比数列的个数是( )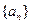 的首项
的首项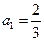 ,
,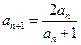 ,
,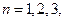 ….证明:数列
….证明:数列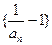 是等比数列;
是等比数列;