题目内容
等差数列{an}的前n项和为Sn,a1=1;等比数列{bn}中,b1=1.若a3+S3=14,b2S2=12.
(I)求an与bn;
(Ⅱ)设cn=an+2bn,数列{cn}的前n项和为Tn.求证:Tn≥3n.
(I)解:设等差数列{an}的公差为d;等比数列{bn}的公比为q,则
∵a3+S3=14,b2S2=12.
∴(1+2d)+(3+3d)=14,d(2+d)=12
∴d=2,q=3
∴an=1+2(n-1)=2n-1,bn=3n-1;
(Ⅱ)证明:∵cn=an+2bn,数列{cn}的前n项和为Tn,
∴Tn=(1+3+…+2n-1)+2(1+3+32+…+3n-1)=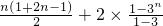 =n2+3n-1≥3n
=n2+3n-1≥3n
∴Tn≥3n
分析:(I)设等差数列{an}的公差为d;等比数列{bn}的公比为q,根据a3+S3=14,b2S2=12,构建方程,即可求an与bn;
(Ⅱ)利用分组求和,求得数列的和,即可证得结论.
点评:本题考查数列的通项与求和,考查方程组的思想,解题的关键是确定数列的通项,属于中档题.
∵a3+S3=14,b2S2=12.
∴(1+2d)+(3+3d)=14,d(2+d)=12
∴d=2,q=3
∴an=1+2(n-1)=2n-1,bn=3n-1;
(Ⅱ)证明:∵cn=an+2bn,数列{cn}的前n项和为Tn,
∴Tn=(1+3+…+2n-1)+2(1+3+32+…+3n-1)=
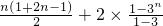 =n2+3n-1≥3n
=n2+3n-1≥3n∴Tn≥3n
分析:(I)设等差数列{an}的公差为d;等比数列{bn}的公比为q,根据a3+S3=14,b2S2=12,构建方程,即可求an与bn;
(Ⅱ)利用分组求和,求得数列的和,即可证得结论.
点评:本题考查数列的通项与求和,考查方程组的思想,解题的关键是确定数列的通项,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设等差数列{an}的前n项和为Sn,则a5+a6>0是S8≥S2的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |