Question

【题目】已知平面内一动点 到点 的距离与点 到 x 轴的距离的差等于1.
（1）求动点 的轨迹 的方程；
（2）过点 作两条斜率存在且互相垂直的直线 ，设 与轨迹 相交于点 ， 与轨迹 相交于点 ，求 的最小值.

Answer 1

【答案】
（1）解：设动点 的坐标为 ，由题意得
化简得 当 时 ；当 时x=0
所以动点P的轨迹 的方程为 和X=0（ ）
（2）解：由题意知，直线 的斜率存在且不为0，设为 ，则 的方程为 ．
由
设 则
，
因为 ，所以 的斜率为 ．设 ，则同理可得 ，



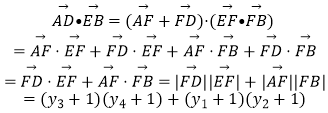
当且仅当 即 时， 取最小值16
【解析】（1）直接设点P的坐标，根据条件设出方程，解出方程即可。
（2）由题意设出两直线方程，分别联立曲线C，根据韦达定理得到坐标间的关系，然后直接求两向量的数量积，在求最值时运用均值不等式即可。