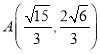题目内容
【题目】我国全面二孩政策已于2016年1月1日起正式实施.国家统计局发布的数据显示,从2012年到2017年,中国的人口自然增长率变化始终不大,在5‰上下波动(如图).

为了了解年龄介于24岁至50岁之间的适孕夫妻对生育二孩的态度如何,统计部门按年龄分为9组,每组选取150对夫妻进行调查统计有生育二孩意愿的夫妻数,得到下表:
年龄区间 |
|
|
|
|
|
|
|
|
|
有意愿数 | 80 | 81 | 87 | 86 | 84 | 83 | 83 | 70 | 66 |
(1)设每个年龄区间的中间值为![]() ,有意愿数为
,有意愿数为![]() ,求样本数据的线性回归直线方程,并求该模型的相关系数
,求样本数据的线性回归直线方程,并求该模型的相关系数![]() (结果保留两位小数);
(结果保留两位小数);
(2)从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
(参考数据和公式: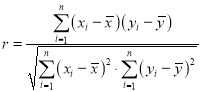 ,
,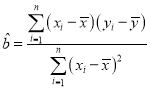 ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)![]() .-0.63(2)
.-0.63(2)![]()
【解析】
(1)根据题意,结合参考数据和公式,代值计算即可求得结果;
(2)列举出所有选取的结果,找出满足题意的选取结果,根据古典概型的概率计算公式即可求得.
解:(1)由题意可求得:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
![]() ,
,
∴![]() .
.
∴![]() .∴
.∴![]() .
.
∴回归直线方程为![]() .
.
∴ .
.
(2)由题意可知,在![]() ,
,![]() ,
,![]() 年龄段中,
年龄段中,
超过半数的夫要有生育二孩意愿,在![]() ,
,![]() 年龄段中,
年龄段中,
超过半数的夫妻没有生育二孩意愿.
设从![]() ,
,![]() ,
,![]() 年龄段中选出的夫妻分别为
年龄段中选出的夫妻分别为![]() ,
,![]() ,
,![]() ,
,
从![]() ,
,![]() 年龄段中选出的夫妻分别为
年龄段中选出的夫妻分别为![]() ,
,![]() .
.
则从中选出2对夫妻的所有可能结果为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10种情况.
,共10种情况.
其中恰有一对不愿意生育二孩的夫妻的情况有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,共6种.
,共6种.
∴恰有一对不愿意生育二孩的夫妻的概率![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知某校运动会男生组田径综合赛以选手三项运动的综合积分高低决定排名.具体积分规则如表1所示,某代表队四名男生的模拟成绩如表2.
表1 田径综合赛项目及积分规则
项目 | 积分规则 |
| 以 |
跳高 | 以 |
掷实心球 | 以 |
表2 某队模拟成绩明细
姓名 | 100米跑(秒) | 跳高(米) | 掷实心球(米) |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根据模拟成绩,该代表队应选派参赛的队员是:( )
A.甲B.乙C.丙D.丁