题目内容
18.已知函数f(x)=ln(x+1)-x2-ax+b在点(0,f(0))处的切线方程为y+2=0.(Ⅰ)求函数f(x)的解析式
(Ⅱ)若函数g(x)=f′(x)+3x在区间(m,2m+1)上不是单调函数,求实数m的取值范围.
分析 (1)根据函数f(x)在x=0处的切线方程为y+2=0,得f(0)=-2,f′(0)=0,求出实数a,b的值即可;
(2)根据函数g(x)在区间(m,2m+1)上不是单调函数,得出g′(m)•g′(2m+1)<0,求出m的取值范围.
解答 解:(Ⅰ)∵函数f(x)=ln(x+1)-x2-ax+b,且x>-1,
∴f′(x)=$\frac{1}{x+1}$-2x-a;
又函数f(x)在点(0,f(0))处的切线方程为y+2=0,
∴f′(0)=1-a=0,解得a=1,
且f(0)=ln1+b=-2,解得b=-2,
∴f(x)=ln(x+1)-x2-x-2;
(Ⅱ)∵f′(x)=$\frac{1}{x+1}$-2x-1(x>-1),
∴g(x)=f′(x)+3x=$\frac{1}{x+1}$-2x-1+3x=$\frac{1}{x+1}$+x-1,
∴g′(x)=-$\frac{1}{{(x+1)}^{2}}$+1(x>-1);
又函数g(x)在区间(m,2m+1)上不是单调函数,
∴g′(m)•g′(2m+1)<0,
即[1-$\frac{1}{{(m+1)}^{2}}$]•[1-$\frac{1}{{(2m+2)}^{2}}$]<0,
∴(1+$\frac{1}{m+1}$)(1-$\frac{1}{m+1}$)(1+$\frac{1}{2(m+1)}$)(1-$\frac{1}{2(m+1)}$)<0;
∵m>-1,∴m+1>0,∴1+$\frac{1}{m+1}$>0,1+$\frac{1}{2(m+1)}$>0,
∴(1-$\frac{1}{m+1}$)(1-$\frac{1}{2(m+1)}$)<0,
即m(2m+1)<0,
解得-$\frac{1}{2}$<m<0,
∴实数m的取值范围(-$\frac{1}{2}$,0).
点评 本题考查了利用函数的导数求曲线的斜率与切线方程的应用问题,也考查了利用函数的导数判断函数的单调性问题,是综合性题目.

| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | b<a<c |
| A. | 1997 | B. | 1999 | C. | 2012 | D. | 2016 |
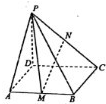 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,M,N分别为AB,PC的中点,PD=AD=2,AB=4.则点A到平面PMN的距离为$\frac{\sqrt{6}}{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,M,N分别为AB,PC的中点,PD=AD=2,AB=4.则点A到平面PMN的距离为$\frac{\sqrt{6}}{3}$.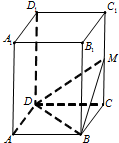 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,点M为CC1的中点,则点D1到平面BDM的距离为$\frac{{2\sqrt{3}}}{3}$.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,点M为CC1的中点,则点D1到平面BDM的距离为$\frac{{2\sqrt{3}}}{3}$.