题目内容
设a>0,函数f(x)=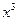 -ax在[1,+∞)上是单调函数.
-ax在[1,+∞)上是单调函数.
(1)求实数a的取值范围;
(2)设 ≥1,f(x)≥1,且f(f(
≥1,f(x)≥1,且f(f( ))=
))= ,求证:f(
,求证:f( )=
)= .
.
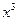 -ax在[1,+∞)上是单调函数.
-ax在[1,+∞)上是单调函数.(1)求实数a的取值范围;
(2)设
 ≥1,f(x)≥1,且f(f(
≥1,f(x)≥1,且f(f( ))=
))= ,求证:f(
,求证:f( )=
)= .
.(1)a的取值范围是(0,3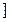 .
.
(2)证明见解析
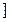 .
.(2)证明见解析
(1)任取
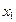 、
、 [1,+∞]且
[1,+∞]且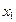 <
<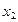 ,则
,则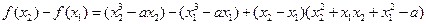 .
.∵
 ,∴
,∴ 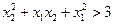 .
.显然,不存在一个常数a,使得
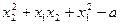 恒为负数.
恒为负数.∵ f(x)有确定的单调性, ∴ 必存在一个常数a,使
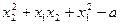 恒为正数,即
恒为正数,即 .
.∴ a≤3,这时有f(
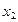 )>f(
)>f(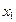 ). ∴ f(x)在[1,+∞
). ∴ f(x)在[1,+∞ 上是增函数,故a的取值范围是(0,3
上是增函数,故a的取值范围是(0,3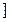 .
.(2)设f(
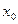 )=u,则f(u)=
)=u,则f(u)=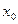 ,于是
,于是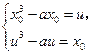
则
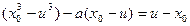 , 即
, 即 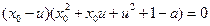 .
.∵
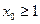 ,
, ,
,  ,
,又∵
 ,∴
,∴ 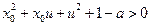 . ∴
. ∴  ,即
,即 ,故
,故 .
.
练习册系列答案
相关题目
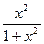

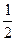 ),f(3)与f(
),f(3)与f(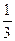 );
);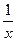 )有什么关系?并证明你的结论;
)有什么关系?并证明你的结论;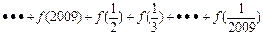 的值.
的值.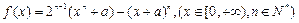 求函数
求函数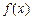 的最小值;
的最小值;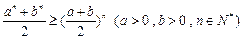 ;
;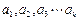 均为正数,则有
均为正数,则有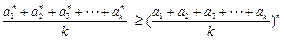 成立(其中
成立(其中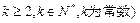 .请你构造一个函数
.请你构造一个函数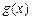 ,证明:
,证明: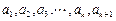 均为正数时,
均为正数时,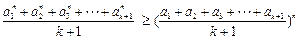 .
.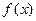 是定义域在
是定义域在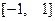 上的奇函数,且其图象上任意两点连线的斜率均小于零.
上的奇函数,且其图象上任意两点连线的斜率均小于零.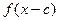 ,
,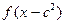 的定义域的交集为空集,求实数
的定义域的交集为空集,求实数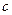 的取值范围;
的取值范围;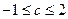 ,则
,则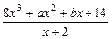 ,定义域为[-1,1]
,定义域为[-1,1]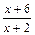 均成立,求实数a,b的值.
均成立,求实数a,b的值.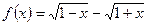 .
.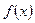 的奇偶性;
的奇偶性;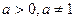 ,解关于
,解关于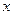 不等式:
不等式: 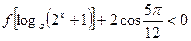 .
. 件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?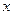 m处的大气压强是
m处的大气压强是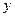 Pa,
Pa,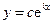 ,其中
,其中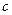 ,
,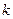 为常量.测得某地某天海平面的大气压强为
为常量.测得某地某天海平面的大气压强为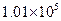 Pa,1000m高空的大气压为
Pa,1000m高空的大气压为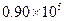 Pa,求600m高空的大气压强(保留
Pa,求600m高空的大气压强(保留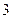 个有效数字).
个有效数字).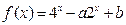 ,当
,当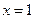 时,
时,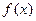 有最小值
有最小值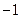 ;
;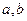 的值; (2)求满足
的值; (2)求满足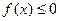 的
的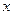 的集合
的集合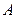 ;
;