题目内容
8.已知△ABC中,∠C=$\frac{π}{2}$,∠A、∠B、∠C对应的边分别为a、b、c,则直线ax+by+c=0被圆x2+y2=4所截得的弦长为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 利用点到直线的距离公式求得圆心到直线ax+by+c=0的距离d,再根据半径r=2,可得弦长.
解答 解:由题意可得a2+b2=c2,圆心(0,0)到直线ax+by+c=0的距离d=$\frac{|0+0+c|}{\sqrt{{a}^{2}+{b}^{2}}}$=1,
再根据半径r=2,可得弦长为2$\sqrt{4-1}$=2$\sqrt{3}$,
故选:D.
点评 本题主要考查圆的标准方程,直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
相关题目
15.已知集合M={x|x2-1≤0},N={x|$\frac{1}{2}$<2x+1<4,x∈Z},则M∩N=( )
| A. | {-1,0} | B. | {1} | C. | {-1,0,1} | D. | ∅ |
19.随机抽查部分成人,得到吸烟与性别的情况如下:
以下哪个值越大,则表明性别与吸烟之间有关系的可能性越大?( )
| 吸烟 | 不吸烟 | |
| 男士 | a | c |
| 女士 | b | d |
| A. | ad-bc | B. | ac-bd | C. | |ad-bc| | D. | |ac-bd| |
3.已知tanα=-$\frac{3}{5}$,则cos2($\frac{π}{4}$+α)=( )
| A. | $\frac{16}{17}$ | B. | $\frac{15}{17}$ | C. | $\frac{9}{17}$ | D. | $\frac{8}{17}$ |
17.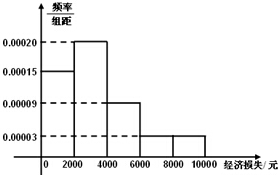 2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图(如图):
2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图(如图):
表一:
(Ⅰ)根据频率分布直方图估计小区平均每户居民的平均损失;
(Ⅱ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50居民捐款情况如表1,在表1表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(Ⅲ)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求连续3天内,有2天李师傅比张师傅早到小区的概率.
附:临界值表参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
 2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图(如图):
2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图(如图):表一:
| 经济损失4000元以下 | 经济损失4000元以上 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款低于500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
(Ⅱ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50居民捐款情况如表1,在表1表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(Ⅲ)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求连续3天内,有2天李师傅比张师傅早到小区的概率.
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |