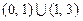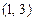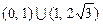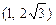题目内容
已知函数f(x)的定义域为R,对任意的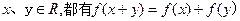 ,且当
,且当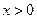 时,
时,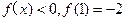 .
.
(Ⅰ)求证:函数f(x)为奇函数;
(Ⅱ)求证: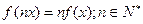
(Ⅲ)求函数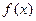 在区间[-n,n](n
在区间[-n,n](n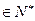 )上的最大值和最小值。
)上的最大值和最小值。
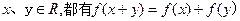 ,且当
,且当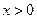 时,
时,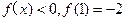 .
.(Ⅰ)求证:函数f(x)为奇函数;
(Ⅱ)求证:
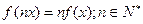
(Ⅲ)求函数
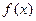 在区间[-n,n](n
在区间[-n,n](n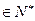 )上的最大值和最小值。
)上的最大值和最小值。(Ⅰ)证明见解析(Ⅱ) 证明见解析(Ⅲ) 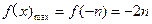 ,
,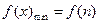 =2n。
=2n。
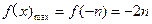 ,
,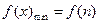 =2n。
=2n。(Ⅰ)证明:∵对任意的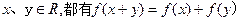 ①
①
令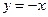 得
得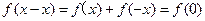 ②…………1分
②…………1分
令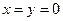 得
得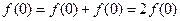 ……………………2分
……………………2分
∴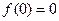 由②得
由②得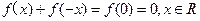
∴函数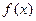 为奇函数………………………………3分
为奇函数………………………………3分
(Ⅱ)证明:(1)当n=1时等式显然成立
(2)假设当n=k(k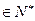 )时等式成立,即
)时等式成立,即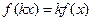 ,…………4分
,…………4分
则当n=k+1时有
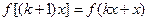 ,由①得
,由①得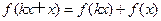 ………………6分
………………6分
∵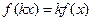 ∴
∴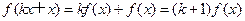
∴当n=k+1时,等式成立。
综(1)、(2)知对任意的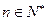 ,
,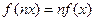 成立。………………8分
成立。………………8分
(Ⅲ)解:设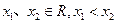 ,因函数
,因函数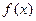 为奇函数,结合①得
为奇函数,结合①得
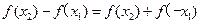 =
=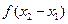 ,……………………9分
,……………………9分
∵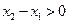
又∵当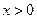 时,
时,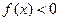
∴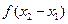
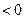 ,∴
,∴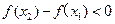
∴函数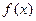 在R上单调递减…………………………………………12分
在R上单调递减…………………………………………12分
∴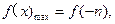
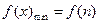
由(2)的结论得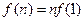 ,
,
∵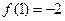 ,∴
,∴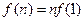 =-2n
=-2n
∵函数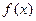 为奇函数,∴
为奇函数,∴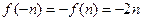
∴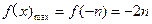 ,
,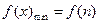 =2n。……………………14分
=2n。……………………14分
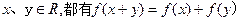 ①
①令
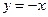 得
得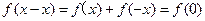 ②…………1分
②…………1分令
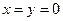 得
得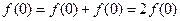 ……………………2分
……………………2分∴
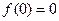 由②得
由②得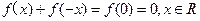
∴函数
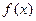 为奇函数………………………………3分
为奇函数………………………………3分(Ⅱ)证明:(1)当n=1时等式显然成立
(2)假设当n=k(k
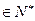 )时等式成立,即
)时等式成立,即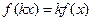 ,…………4分
,…………4分则当n=k+1时有
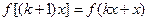 ,由①得
,由①得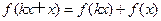 ………………6分
………………6分∵
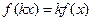 ∴
∴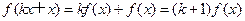
∴当n=k+1时,等式成立。
综(1)、(2)知对任意的
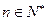 ,
,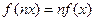 成立。………………8分
成立。………………8分(Ⅲ)解:设
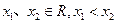 ,因函数
,因函数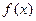 为奇函数,结合①得
为奇函数,结合①得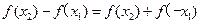 =
=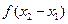 ,……………………9分
,……………………9分∵
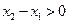
又∵当
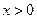 时,
时,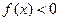
∴
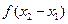
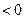 ,∴
,∴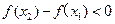
∴函数
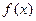 在R上单调递减…………………………………………12分
在R上单调递减…………………………………………12分∴
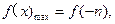
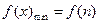
由(2)的结论得
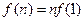 ,
,∵
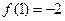 ,∴
,∴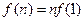 =-2n
=-2n∵函数
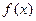 为奇函数,∴
为奇函数,∴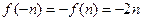
∴
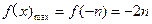 ,
,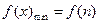 =2n。……………………14分
=2n。……………………14分
练习册系列答案
相关题目
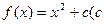 为实常数),且
为实常数),且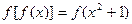 ,其图象和y轴交于A点;数列
,其图象和y轴交于A点;数列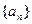 为公差为
为公差为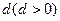 的等差数列,且
的等差数列,且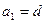 ;点列
;点列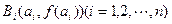
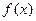 的表达式;
的表达式;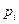 为直线
为直线 的斜率,
的斜率,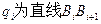 的斜率,求证数
的斜率,求证数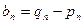 仍为等差数列;
仍为等差数列;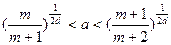 ,求证数列
,求证数列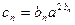 有唯一的最大项.
有唯一的最大项.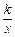 +
+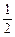 x2在 (0,
x2在 (0,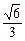 ]上是单调减函数,求实数k的取值范围;
]上是单调减函数,求实数k的取值范围;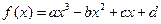 (a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值
(a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值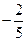 .
.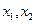 ∈[-1,1],不等式
∈[-1,1],不等式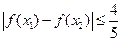 成立;
成立;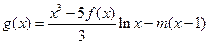 在区间(1,∞)内无零点,求实数m的取值范围.
在区间(1,∞)内无零点,求实数m的取值范围.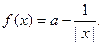
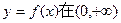 上是增函数.
上是增函数. 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.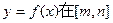 上的值域是
上的值域是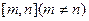 ,求实数a的取值范围.
,求实数a的取值范围.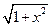 定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.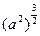 =a3 ②
=a3 ②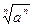 =|a| ③函数y=
=|a| ③函数y=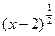 -(3x-7)0的定义域是(2, +∞) ④若
-(3x-7)0的定义域是(2, +∞) ④若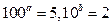 ,则2a+b=1
,则2a+b=1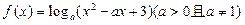 ,满足对任意的
,满足对任意的 、
、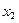 ,当
,当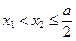 时,
时,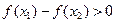 ,则实数
,则实数 的取值范围为( )
的取值范围为( )