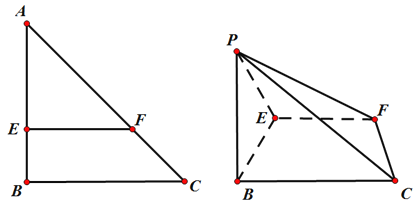
题目内容
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 离心率为
离心率为![]() ,两准线之间的距离为8,点
,两准线之间的距离为8,点![]() 在椭圆
在椭圆![]() 上,且位于第一象限,过点
上,且位于第一象限,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 的交点
的交点![]() 在椭圆
在椭圆![]() 上,求点
上,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由椭圆的离心率公式求得![]() ,由椭圆的准线方程
,由椭圆的准线方程![]() ,则
,则![]() ,即可求得
,即可求得![]() 和
和![]() 的值,则
的值,则![]() ,即可求得椭圆方程;(2)设
,即可求得椭圆方程;(2)设![]() 点坐标,分别求得直线
点坐标,分别求得直线![]() 的斜率及直线
的斜率及直线![]() 的斜率,则可求得
的斜率,则可求得![]() 及
及![]() 的斜率及方程,联立求得
的斜率及方程,联立求得![]() 点坐标,由
点坐标,由![]() 满足椭圆方程,求得
满足椭圆方程,求得![]() ,结合
,结合![]() 在椭圆E上,
在椭圆E上,![]() 联立即可求得
联立即可求得![]() 点坐标.
点坐标.
试题解析:(1)设椭圆的半焦距为c.因为椭圆E的离心率为![]() ,两准线之间的距离为8,所以
,两准线之间的距离为8,所以![]() ,
,![]() ,解得
,解得![]() ,于是
,于是![]() ,因此椭圆E的标准方程是
,因此椭圆E的标准方程是![]() .
.
(2)由(1)知,![]() ,
,![]() .设
.设![]() ,因为
,因为![]() 为第一象
为第一象
限的点,故![]() .当
.当![]() 时,
时,![]() 与
与![]() 相交于
相交于![]() ,与题设不符.
,与题设不符.
当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
, ![]() 直线
直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
从而直线![]() 的方程
的方程![]() ,① 直线
,① 直线![]() 的方程
的方程![]() ,②
,②
由①②,解得![]() ,所以
,所以![]() .因为点
.因为点![]() 在椭圆上,由对称性,得
在椭圆上,由对称性,得![]() ,即
,即![]() 或
或![]() .又
.又![]() 在椭圆E上,故
在椭圆E上,故![]() .
.
由 ,解得
,解得![]() ;
;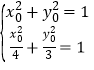 ,无解.因此点P的坐标为
,无解.因此点P的坐标为![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.

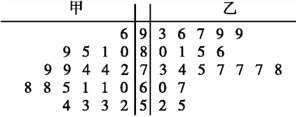
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了![]() 人,将调查情况进行整理后制成下表:
人,将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
(![]() )完成被调查人员的频率分布直方图.
)完成被调查人员的频率分布直方图.
(![]() )若从年龄在
)若从年龄在![]() ,
,![]() 的被调查者中各随机选取
的被调查者中各随机选取![]() 人进行追踪调查,求恰有
人进行追踪调查,求恰有![]() 人不赞成的概率.
人不赞成的概率.
(![]() )在
)在![]() 在条件下,再记选中的
在条件下,再记选中的![]() 人中不赞成“车辆限行”的人数为
人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.