题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)函数![]() 的图象能否与
的图象能否与![]() 轴相切?若能,求出实数
轴相切?若能,求出实数![]() ,若不能,请说明理由;
,若不能,请说明理由;
(Ⅱ)求最大的整数![]() ,使得对任意
,使得对任意![]() ,不等式
,不等式![]() 恒成立.
恒成立.
【答案】(Ⅰ)答案见解析;(Ⅱ)3.
【解析】试题分析:
(Ⅰ)若能与![]() 轴相切,则存在
轴相切,则存在![]() ,使得
,使得![]() ,能求出
,能求出![]() ,说明存在,否则说明不存在;
,说明存在,否则说明不存在;
(Ⅱ)把已知不等式变形为![]() ,由于
,由于![]() ,因此只要函数
,因此只要函数![]() 是增函数即可,由
是增函数即可,由![]() 中
中![]() 得
得![]() ,这是必要条件,其中最大整数是3,因此下面只要证
,这是必要条件,其中最大整数是3,因此下面只要证![]() 时,
时,![]() 恒成立.为此可分类,
恒成立.为此可分类,![]() 时,
时,![]() ,代入可证有,
,代入可证有,![]() 时,由
时,由![]() 可证
可证![]() ,从而可得结论.
,从而可得结论.
试题解析:
(Ⅰ)由于![]() .
.
假设函数![]() 的图象与
的图象与![]() 轴相切于点
轴相切于点![]() ,
,
则有![]() ,即
,即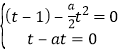 .
.
显然![]() 代入方程
代入方程![]() 中得,
中得,![]() .
.
∵![]() ,∴无解.故无论
,∴无解.故无论![]() 取何值,函数
取何值,函数![]() 的图象都不能与
的图象都不能与![]() 轴相切.
轴相切.
(Ⅱ)依题意,![]()
![]() 恒成立.
恒成立.
设![]() ,则上式等价于
,则上式等价于![]() ,要使
,要使![]()
对任意![]() 恒成立,即使
恒成立,即使![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上恒成立.
上恒成立.
则![]() ,∴
,∴![]() 在
在![]() 上成立的必要条件是:
上成立的必要条件是:![]() .
.
下面证明:当![]() 时,
时,![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() .那么,
.那么,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() 恒成立.
恒成立.
因此,![]() 的最大整数值为 3.
的最大整数值为 3.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目