题目内容
【题目】(本小题满分12分)
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=![]() .
.
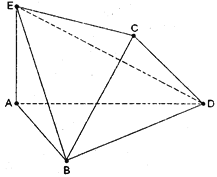
(Ⅰ)求证:DE⊥AC;
(Ⅱ)求DE与平面BEC所成角的正弦值;
(Ⅲ)直线BE上是否存在一点M,使得CM∥平面ADE,若存在,求点M的位置,不存在请说明理由.
【答案】(1)以A为原点,以射线AB,AC,AE为坐标轴建立空间直角坐标系,
则![]() 由C作平面ABD的垂线,垂足为F,则F为BC的中点,
由C作平面ABD的垂线,垂足为F,则F为BC的中点,![]() ,所以点C的坐标为
,所以点C的坐标为![]() ,
,![]()
![]()
故:DE⊥AC(2)![]() (3)存在M为BE的中点,使得CM//平面ADE
(3)存在M为BE的中点,使得CM//平面ADE
【解析】
试题以A为原点,以射线AB,AC,AE为坐标轴建立空间直角坐标系,
则![]()
由C作平面ABD的垂线,垂足为F,则F为BC的中点,![]() ,
,
所以点C的坐标为![]() 。
。
(1)![]()
![]() ,故:DE⊥AC。
,故:DE⊥AC。
(2)![]()
设平面BCE的法向量为![]() ,则
,则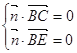 ,
,![]()
设线面角为![]() ,
,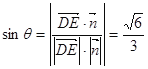
(3)设![]() ,则
,则![]() 。若CM//平面ADE,则
。若CM//平面ADE,则![]() ,所以
,所以![]() ,故存在M为BE的中点,使得CM//平面ADE。
,故存在M为BE的中点,使得CM//平面ADE。

练习册系列答案
相关题目

