题目内容
7．在△ABC中，a=3，b=x，cosB=$\frac{2}{3}$，若△ABC有两解，则x的取值范围是（ ）| A． | （3，+∞） | B． | （$\sqrt{5}$，+∞） | C． | （$\sqrt{5}$，3） | D． | （0，$\sqrt{5}$） |
分析 △ABC有两解时需要：bsinA＜a＜b，代入数据，求出x的范围．
解答 解：由题意得，△ABC有两解时需要：bsinA＜a＜b，
则xsinA＜3＜x，解得3＜x＜$\frac{3}{sinA}$，
所以x的取值范围是（3，$\frac{3}{sinA}$），
比较各个选项可得（3，+∞），
故选：A．
点评 本题考查了解三角形一题多解的问题，注意理解，属于基础题．
练习册系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
15．若直线ax+y+1=0与直线y=3x-2平行，则实数a=（ ）
| A． | -3 | B． | -$\frac{1}{3}$ | C． | 3 | D． | $\frac{1}{3}$ |
2．在等比数列{an}中，若a5，a6是方程x2-4x+1=0的两个根，则a4•a7=（ ）
| A． | 2 | B． | -1 | C． | 1 | D． | ±1 |
12．下列各组向量中，可以作为基底的是（ ）
| A． | $\overrightarrow{{e}_{1}}$=（-1，2），$\overrightarrow{{e}_{2}}$=（5，7） | B． | $\overrightarrow{{e}_{1}}$=（0，0），$\overrightarrow{{e}_{2}}$=（1，-2） | ||
| C． | $\overrightarrow{{e}_{1}}$=（3，5），$\overrightarrow{{e}_{2}}$=（6，10） | D． | $\overrightarrow{{e}_{1}}$=（2，-3），$\overrightarrow{{e}_{2}}$=（$\frac{1}{2}$，-$\frac{3}{4}$） |
19．来晋江旅游的外地游客中，若甲、乙、丙三人选择去五店市游览的概率均为$\frac{3}{5}$，且他们的选择互不影响，则这三人中至多有两人选择去五店市游览的概率为（ ）
| A． | $\frac{36}{125}$ | B． | $\frac{44}{125}$ | C． | $\frac{54}{125}$ | D． | $\frac{98}{125}$ |
16．若某空间几何体的三视图如图所示，则该几何体的体积是（ ）
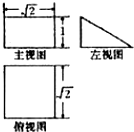
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | 1 |
17．下列说法不正确的是（ ）
| A． | 若“p且q”为假，则p，q至少有一个是假命题 | |
| B． | 命题“?x∈R，x2-x-1＜0”的否定是““?x∈R，x2-x-1≥0” | |
| C． | 当a＜0时，幂函数y=xa在（0，+∞）上单调递减 | |
| D． | “φ=$\frac{π}{2}$”是“y=sin（2x+φ）为偶函数”的充要条件 |