题目内容
【题目】咖啡馆配制两种饮料,甲种饮料分别用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。乙种饮料分别用奶粉
。乙种饮料分别用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。已知每天使用原料限额为奶粉
。已知每天使用原料限额为奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。如果甲种饮料每杯能获利
。如果甲种饮料每杯能获利![]() 元,乙种饮料每杯能获利
元,乙种饮料每杯能获利![]() 元。每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
元。每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
【答案】每天应配制甲种饮料200杯,乙种饮料240杯,能使该咖啡馆获利最大
【解析】试题分析: 首先设每天应配制甲种饮料![]() 杯,乙种饮料
杯,乙种饮料![]() 杯,咖啡馆每天获利
杯,咖啡馆每天获利![]() 元,建立目标函数
元,建立目标函数![]() ,求出
,求出![]() 满足 的线性约束条件,画出可行域,找到最优解.
满足 的线性约束条件,画出可行域,找到最优解.
试题解析 :设每天配制甲种饮料![]() 杯,乙种饮料
杯,乙种饮料![]() 杯,咖啡馆每天获利
杯,咖啡馆每天获利![]() 元,则
元,则![]() 、
、![]() 满足约束条件:
满足约束条件:
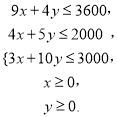
目标函数![]()
在平面直角坐标系内作出可行域,如图:
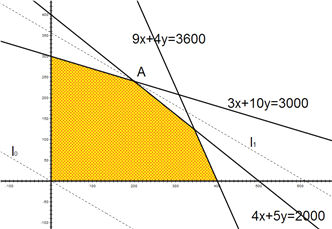
作直线![]() :
: ![]() ,把直线
,把直线![]() 向右上方平移至
向右上方平移至![]() 的位置时,直线经过可行域上的
的位置时,直线经过可行域上的![]() 点,且与原点距离最大,此时
点,且与原点距离最大,此时![]() 取最大值。
取最大值。
解方程组![]() ,得
,得![]() 点坐标
点坐标![]() 。
。
答:每天应配制甲种饮料200杯,乙种饮料240杯,能使该咖啡馆获利最大。

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目