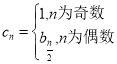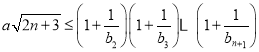题目内容
【题目】如图：已知某公园的四处景观分别位于等腰梯形
的四个顶点处，其中
，
两地的距离为
千米，
，
两地的距离为
千米，
.现拟规划在
(不包括端点)路段上增加一个景观
，并建造观光路直接通往处，造价为每千米
万元，又重新装饰
路段，造价为每千米
万元.
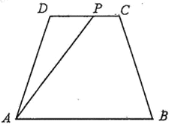
(1)若拟修建观光路
路段长为
千米，求路段的造价；
(2)设
，当
为何值时，，段的总造价最低.
【答案】（1）
万元；
（2）
；
【解析】
（1）结合等腰梯形的性质和余弦定理即可求解；
（2）结合正弦定理代换出
，进而表示出
，列出总造价的表达式，结合导数即可求解
(1) 如图:
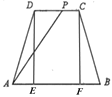
作
，
，垂足分别为
，
，
则有
，所以
，所以
.
设
，
在三角形
中，由余弦定理
得到
，整理得到
所以
或
(舍去)
所以
，段造价为万元.
故段造价为万元.
(2)因为在三角形中，
，
，
所以
，由正弦定理得，
，
所以
，
.
设总造价为
，则
，
则有
，
令
，得
，令
，
列表：
|
|
|
|
|
|
|
|
|
| 极小值 |
|
由列表当
，即时，有最小值.
故当时，
，段的总造价最低.
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
