题目内容
(本题满分14分)设函数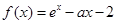 ,
,
(1)求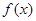 的单调区间
的单调区间
(2)若 为整数,且当
为整数,且当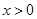 时,
时,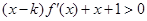 ,求
,求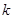 的最大值.
的最大值.
【答案】
(1)若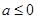 ,
,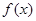 在(-∞,+∞)上单调递增;若
在(-∞,+∞)上单调递增;若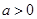 ,
,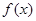 在
在 单调递减,在
单调递减,在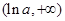 上单调递增;(2)
上单调递增;(2)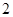
【解析】
试题分析:(1)函数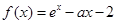 的定义域是
的定义域是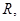
 ,
,
若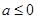 ,则
,则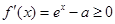 ,所以函数
,所以函数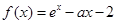 在(-∞,+∞)上单调递增.
在(-∞,+∞)上单调递增.
若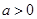 ,则当
,则当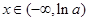 时,
时, ;
;
当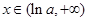 时,
时,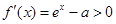 ;所以,
;所以,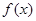 在
在 单调递减,在
单调递减,在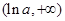 上单调递增. ……6分
上单调递增. ……6分
(II)由于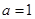 ,所以,
,所以,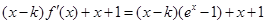 ,
,
故当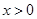 时,
时,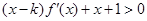 等价于
等价于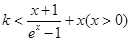 ①
①
令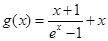 ,则
,则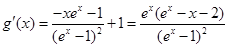
由(I)知,函数 在
在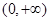 上单调递增,而
上单调递增,而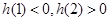 ,
,
所以 在
在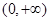 上存在唯一的零点,
上存在唯一的零点,
故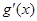 在
在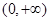 上存在唯一的零点,
上存在唯一的零点,
设此零点为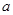 ,则有
,则有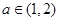 ,
,
当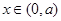 时,
时,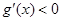 ;当
;当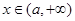 时,
时, ;所以
;所以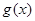 在
在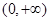 上的最小值为
上的最小值为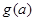 .又由
.又由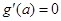 ,可得
,可得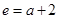 ,所以
,所以 ,
,
由于①式等价于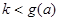 ,故整数
,故整数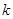 的最大值为
的最大值为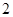 . ……14分
. ……14分
考点:本小题主要考查利用导数研究函数的单调性、构造新函数求解恒成立问题,考查学生构造函数的能力和分类讨论思想的应用以及运算求解能力.
点评:函数的单调性、极值、最值问题一般都要借助于导数这个工具,而恒成立问题一般转化为求最值问题解决.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 的左、右焦点分别为F1与
的左、右焦点分别为F1与 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。 变成曲线
变成曲线 ,直线
,直线 与曲线
与曲线 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点) 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 满足
满足 ”
” 是集合M中的元素;
是集合M中的元素;
 ,都存在
,都存在 ,使得等式
,使得等式 成立。
成立。  .
. ,求函数
,求函数 的极值;
的极值; ,试确定
,试确定 的单调性;
的单调性; ,且
,且 在
在 上的最大值为M,证明:
上的最大值为M,证明: .
.