题目内容
（本题满分14分）设函数
（1）求函数
的单调区间；（2）求在[—1，2]上的最小值； （3）当
时，用数学归纳法证明：
(Ⅰ) 增区间为
… (Ⅱ) 见解析
解析:
（1）
…………2分
令
|
|
| —2 | （-2，0） | 0 | （0，1） | 1 |
|
|
| — | 0 | + | 0 | — | 0 | + |
|
| 减 | 极小 | 增 | 极大 | 减 | 极小 | 增 |
函数的增区间为
…………5分
（2）当
所以
………………8分
（3）设
； ………………10分
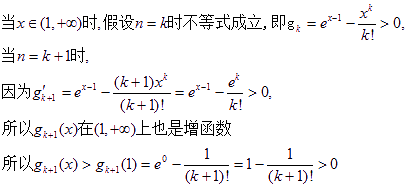
即当
时，不等式成立。
所以当时，
………………14分
练习册系列答案
相关题目
，
。
，过两点
和
的中点作
轴的垂线交曲线
于点
，求证：曲线
处的切线
过点
；
，当
时
恒成立，求实数
的取值范围。
的左、右焦点分别为F1与
过椭圆的一个焦点F2且与椭圆交于P、Q两点，若
的周长为
。
变成曲线
，直线
与曲线
，求
面积的取值范围。（O为坐标原点）
构成的集合：“①方
有实数根；②函数
满足
”
是集合M中的元素；
，都存在
，使得等式
成立。 
.
，求函数
的极值；
，试确定
的单调性；
，且
在
上的最大值为M，证明：
．