题目内容
本题满分14分)
设函数 .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)若 ,试确定
,试确定 的单调性;
的单调性;
(3)记 ,且
,且 在
在 上的最大值为M,证明:
上的最大值为M,证明: .
.
【答案】
解:(1)若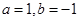 ,则
,则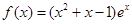
有
令 得
得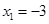 ,
,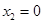 -------------------------------------------1分
-------------------------------------------1分
∵当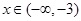 时
时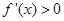 ,当
,当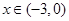 时
时 ,当
,当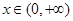 时,
时,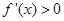
∴当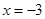 时,函数
时,函数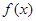 有极大值,
有极大值,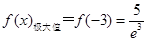 ,-----------------------------2分
,-----------------------------2分
当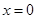 时,函数
时,函数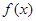 有极小值,
有极小值,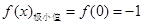 --------------------------------3分
--------------------------------3分
(2)∵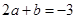 即
即 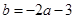
又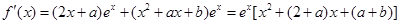
∴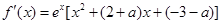 =
=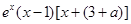 --------------------------------5分
--------------------------------5分
当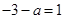 即
即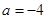 时,
时,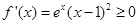
∴函数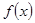 在
在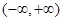 上单调递增;--------------------------------------------------------------6分
上单调递增;--------------------------------------------------------------6分
当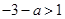 ,即
,即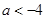 时,由
时,由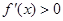 得
得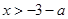 或
或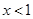 ,
,
由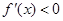 得
得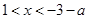 ;------------------------------------------------------------------------7分
;------------------------------------------------------------------------7分
当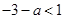 ,即
,即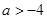 时,由
时,由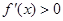 得
得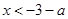 或
或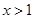 ,
,
由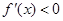 得
得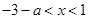 ;------------------------------------------------------------------------8分
;------------------------------------------------------------------------8分
综上得:当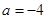 时,函数
时,函数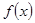 在
在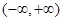 上单调递增;
上单调递增;
当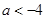 时,函数
时,函数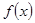 在
在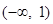 和
和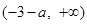 上单调递增,在
上单调递增,在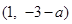 上单调递减-9分
上单调递减-9分
当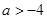 时,函数
时,函数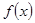 在
在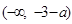 和
和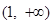 上单调递增,在
上单调递增,在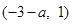 上单调递减.---10分
上单调递减.---10分
(3)根据题意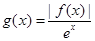 =
=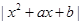 ,
,
∵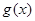 在
在 上的最大值为M,
上的最大值为M,
∴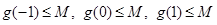
即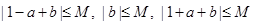 --------------------------------------12分
--------------------------------------12分
2=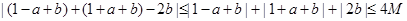
∴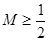 ---------------------------------------------14分
---------------------------------------------14分
【解析】略

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 的左、右焦点分别为F1与
的左、右焦点分别为F1与 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。 变成曲线
变成曲线 ,直线
,直线 与曲线
与曲线 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点) 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 满足
满足 ”
” 是集合M中的元素;
是集合M中的元素;
 ,都存在
,都存在 ,使得等式
,使得等式 成立。
成立。