题目内容
已知f(x)=|lgx|,且0<a<b<c,若?f(b)<f(a)<f(c),则下列一定成立的是( )
| A.a<1,b<1,且c>1 | B.0<a<1,b>1且c>1 |
| C.b>1,c>1 | D.c>1且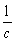 <a<1,a<b< <a<1,a<b<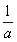 |
D
分析:由绝对值得意义,去绝对值进行讨论得出ab的关系即可
解答:解:∵f(x)=|lgx|,0<a<b<c,f(b)<f(a)<f(c),
若0<a<b<c<1,则f(a)>f(b)>f(c),与题意不符;
若1<a<b<c,应有f(a)<f(b)<f(c),与题意不符;
∴0<a<1,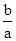 >1,c>1.b与1的大小关系不定,可排除A、B、C.
>1,c>1.b与1的大小关系不定,可排除A、B、C.
∴f(b)<f(a)<f(c)?|lgb|<|lga|<lgc,
∵|lgb|<|lga|,
∴lg2b<lg2a,即(lga+lab)?(lgb-lga)<0,lgab?lg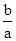 <0,由
<0,由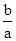 >1得lg
>1得lg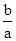 >0,
>0,
∴lgab<0,∴0<ab<1,
∴a<b<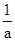 ①,又|lga|<lgc,而|lga|=-lga=lg
①,又|lga|<lgc,而|lga|=-lga=lg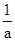 ,∴0<lg
,∴0<lg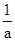 <lgc,
<lgc,
∴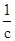 <a<1,②又c>1,
<a<1,②又c>1,
由①②可得D正确.
故选D.
点评:本题考查绝对值得意义、对数的取值和运算、比较大小等知识,考查对数的性质与转化、运算能力,属于难题.
解答:解:∵f(x)=|lgx|,0<a<b<c,f(b)<f(a)<f(c),
若0<a<b<c<1,则f(a)>f(b)>f(c),与题意不符;
若1<a<b<c,应有f(a)<f(b)<f(c),与题意不符;
∴0<a<1,
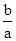 >1,c>1.b与1的大小关系不定,可排除A、B、C.
>1,c>1.b与1的大小关系不定,可排除A、B、C.∴f(b)<f(a)<f(c)?|lgb|<|lga|<lgc,
∵|lgb|<|lga|,
∴lg2b<lg2a,即(lga+lab)?(lgb-lga)<0,lgab?lg
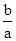 <0,由
<0,由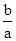 >1得lg
>1得lg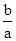 >0,
>0,∴lgab<0,∴0<ab<1,
∴a<b<
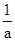 ①,又|lga|<lgc,而|lga|=-lga=lg
①,又|lga|<lgc,而|lga|=-lga=lg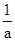 ,∴0<lg
,∴0<lg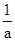 <lgc,
<lgc,∴
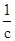 <a<1,②又c>1,
<a<1,②又c>1,由①②可得D正确.
故选D.
点评:本题考查绝对值得意义、对数的取值和运算、比较大小等知识,考查对数的性质与转化、运算能力,属于难题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
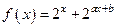 ,且f(1)=
,且f(1)=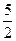 ,f(2)=
,f(2)=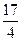 .(1)求
.(1)求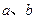 ;(2)判断
;(2)判断 f(x)的奇偶性;(3)试判断函数在
f(x)的奇偶性;(3)试判断函数在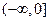 上的单调性,并证明。
上的单调性,并证明。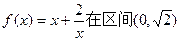 上是减函数.
上是减函数.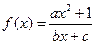 是奇函数(a,b,c都是整数),且
是奇函数(a,b,c都是整数),且
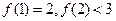 ,
,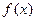 的单调性如何?用单调性定义证明你的结论。
的单调性如何?用单调性定义证明你的结论。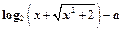 为奇
为奇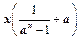 为偶函数,证明你的结论。
为偶函数,证明你的结论。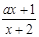 在区间(-2,+∞)上单调递增,则实数a的取值范围是( )
在区间(-2,+∞)上单调递增,则实数a的取值范围是( )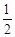 )
) 的反函数的图象关于点(–2,3)对称,则f(x)的单调性为 ( )
的反函数的图象关于点(–2,3)对称,则f(x)的单调性为 ( )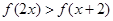 的解集是( )
的解集是( )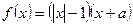 为奇函数,则
为奇函数,则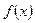 增
增 区间为________.
区间为________.