题目内容
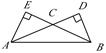
如图，在△ABC中，∠CAB＝∠CBA＝30°，AC、BC边上的高分别为BD、AE，则以A、B为焦点，且过D、E的椭圆与双曲线的离心率分别为
，则
．
，则 ．
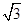
试题分析：设
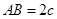，则椭圆中
，
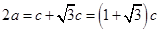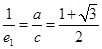，双曲线中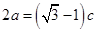
，
，
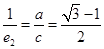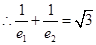
点评：求离心率主要需要找关于
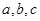的关系式，本题中利用椭圆和双曲线的定义分别求出
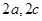的关系，从而求得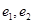
练习册系列答案
名校课堂系列答案
相关题目
试题分析：设
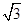
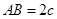，则椭圆中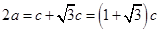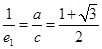，，双曲线中，，点评：求离心率主要需要找关于
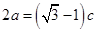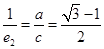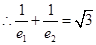
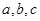的关系式，本题中利用椭圆和双曲线的定义分别求出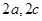的关系，从而求得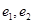名校课堂系列答案
过点
，其长轴、焦距和短轴的长的平方依次成等差数列．
轴正半轴、
轴分别交于点
，与椭圆分别交于点
，各点均不重合，且满足
，
． 当
时，试证明直线过定点．过定点（1，0）
，短轴长为4
.
，直线PB的斜率为
，判断
的焦点坐标是 （ ）
分别是椭圆
的左右焦点，过
与
轴垂直的直线交椭圆于
两点，若
是锐角三角形，则椭圆离心率的范围是（ ）
的中心在坐标原点，焦点在
轴上，其左、右焦点分别为
、
，短轴长为
，点
在椭圆
的周长为6．
的直线与椭圆相交于A、B两点，试问在x轴上是否存在一个定点M使
恒为定值？若存在求出该定值及点M的坐标，若不存在请说明理由．
，（
为参数）的普通方程为 （ ）
．
，判断点P与直线l的位置关系；
，
；
的焦点为F，点
为该抛物线上的动点，又点
则
的最小值是
