题目内容
3.已知点P(x,y)满足$\left\{\begin{array}{l}{y≤2x}\\{y≥0}\\{3x-y-6≤0}\end{array}\right.$,则点P到直线y=x距离的最大值等于3$\sqrt{2}$.分析 作出不等式组对应的平面区域,利用点到直线的距离结合数形结合进行求解即可.
解答 解:作出不等式组对应的平面区域如图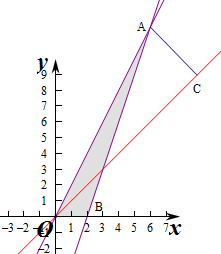 :
:
由图象可知点A到直线y=x的距离最大,
由$\left\{\begin{array}{l}{y=2x}\\{3x-y-6=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=6}\\{y=12}\end{array}\right.$,
即A(6,12),
则A到直线x-y=0的距离d=$\frac{|6-12|}{\sqrt{2}}=\frac{6}{\sqrt{2}}$=3$\sqrt{2}$,
故答案为:3$\sqrt{2}$.
点评 本题主要考查线性规划一件点到直线距离公式的应用,利用数形结合确定距离最远的点是解决本题的关键.

练习册系列答案
相关题目
14.设a1,a2…,an…是按先后顺序排列的一列向量,若a1=(-2015,14),且an-an-1=(1,1),则其中模最小的一个向量的序号n=( )
| A. | 2015 | B. | 2014 | C. | 1007或1008 | D. | 1001或1002 |
18.设实数a满足a∈[0,π],若函数f(x)=sinx+sin(x+a)-1没有零点,则实数a的取值范围是( )
| A. | ($\frac{2π}{3}$,π] | B. | (0,$\frac{2π}{3}$) | C. | ($\frac{π}{6}$,π] | D. | ($\frac{π}{6}$,$\frac{π}{2}$] |