题目内容
3.如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=2,AD=CD=1,点E、F分别为AB、BC的中点,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.(1)求证:BC⊥平面ACD;
(2)求几何体D-ABC的体积;
(3)在线段BD上是否存在一点G,使得平面GEF∥平面ACD,若存在,试确定点G的位置并予以证明,若不存在,请说明理由.
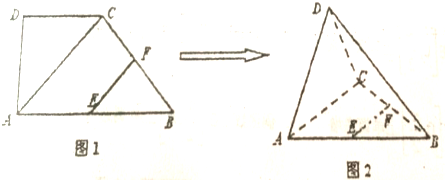
分析 (1)由题意知,AC=BC=$\sqrt{2}$,由勾股定理可得AC⊥BC,取AC中点O,连接DO,由面面垂直的性质得OD⊥平面ABC,再由线面垂直的判断得答案;
(2)(1)知,BC为三棱锥B-ACD的高,求出三棱锥B-ACD的体积,由等积法可得D-ABC的体积;
(3)取G为线段BD的中点,连接EF、EG、FG,由三角形的中位线定理结合面面平行的判定得答案.
解答 (1)证明: 在图1中,由题意知,AC=BC=$\sqrt{2}$,∴AC2+BC2=AB2,∴AC⊥BC,
在图1中,由题意知,AC=BC=$\sqrt{2}$,∴AC2+BC2=AB2,∴AC⊥BC,
取AC中点O,连接DO,则DO⊥AC,又平面ADC⊥平面ABC,
且平面ADC∩平面ABC=AC,DO?平面ACD,从而OD⊥平面ABC,
∴OD⊥BC,
又AC⊥BC,AC∩OD=O,
∴BC⊥平面ACD;
(2)解:由(Ⅰ)知,BC为三棱锥B-ACD的高,且BC=$\sqrt{2}$,S△ACD=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
∴三棱锥B-ACD的体积为:VB-ACD=$\frac{1}{3}$Sh=$\frac{1}{3}$×$\frac{1}{2}×\sqrt{2}$=$\frac{\sqrt{2}}{6}$,
由等积性知几何体D-ABC的体积为:$\frac{\sqrt{2}}{6}$;
(3)解:若G为线段BD的中点,则平面GEF∥平面ACD.
证明:取G为线段BD的中点,连接EF、EG、FG,
∵点E、F、G分别为AB、BC、BD的中点,∴EF∥AC,EG∥AD,
AC?面ACD,AD?面ACD,EF?面ACD,EG?面ACD,
∴EF∥面ACD,EG∥面ACD,又EF∩EG=E,
∴平面GEF∥平面ACD.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案| A. | 若α⊥β,m∥α,则m⊥β | B. | 若m∥α,n∥m,则n∥α | ||
| C. | 若m∥α,n∥β,且m∥n,则α∥β | D. | 若m⊥β,m∥α,则α⊥β |
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 4 |
| A. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{3}$] | B. | (0,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{2}}{3}$,$\frac{\sqrt{3}}{3}$] |
(Ⅰ)当a=1时,求f(x)的最大值;
(Ⅱ)当x∈(-∞,0)∪(0,+∞)时,$\frac{f(x)}{x}$<1恒成立,证明:a=1.
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |