题目内容

11．已知不等式x2-ax+a-2＞0（a＞2）的解集为（-∞，x1）∪（x2，+∞），则x1+x2+$\frac{1}{{x}_{1}{x}_{2}}$的最小值为（　　）
A．$\frac{1}{2}$B．2C．$\frac{5}{2}$D．4

分析 先根据由韦达定理x1+x2=a，x1x2=a-2，再根据基本不等式即可求出最小值．

解答 解：a＞2时，△=a2-4（a-2）＞0，由韦达定理x1+x2=a，x1x2=a-2，
则x1+x2+$\frac{1}{{x}_{1}{x}_{2}}$=$a+\frac{1}{a-2}=a-2+\frac{1}{a-2}+2≥4$，当且仅当a=3时取等号．
故选：D．

点评 本题考查了一元二次不等式的解集和基本不等式的性质，属于基础题．

练习册系列答案
相关题目
1．设数列{an}的前n项和为Sn，且Sn满足3n2-n=2Sn，n∈N*．
（1）求数列{an}的通项公式；
（2）设bn=$\frac{{a}_{n}+2}{{3}^{n+1}}$，求数列{bn}的前n项和Tn．
2．阅读如图的程序框图，当程序运行后，输出S的值为（　　）
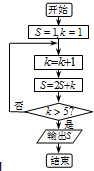
A．57B．119C．120D．247
19．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-1（x≤0）}\\{f（x-1）+1（x＞0）}\end{array}\right.$，g（x）=f（x）-x，把函数g（x）的零点按从小到大的顺序排列成一个数列，则该数的前n项和为（　　）
A．Sn=$\frac{n（n-1）}{2}$B．Sn=$\frac{n（n+1）}{2}$C．Sn=2n-1D．Sn=2n-1-1
6．复数z满足z（$\overline{z}$+1）=1+i，其中i是虚数单位，则z=（　　）
A．1+i或-2+iB．i或1+iC．i或-1+iD．-1-i或-2+i
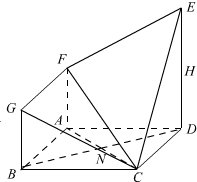16．在如图所示的几何体ABCDEFG中，四边形ABCD是边长为4的正方形，DE⊥平面ABCD，DE∥AF∥BG，H是DE的中点，AC与BD相交于N，DE=2AF=2BG=4
（Ⅰ）在FH上求一点P，使NP∥平面EFC；
（Ⅱ）求二面角E-FC-G的余弦值．
3．如图1，在直角梯形ABCD中，∠ADC=90°，CD∥AB，AB=2，AD=CD=1，点E、F分别为AB、BC的中点，将△ADC沿AC折起，使平面ADC⊥平面ABC，得到几何体D-ABC，如图2所示．
（1）求证：BC⊥平面ACD；
（2）求几何体D-ABC的体积；
（3）在线段BD上是否存在一点G，使得平面GEF∥平面ACD，若存在，试确定点G的位置并予以证明，若不存在，请说明理由．
14．已知函数f（x）=ln（x-1）+$\frac{2a}{x}$（a∈R）
（Ⅰ）若a=3，求f（x）的单调区间；
（Ⅱ）如果当x＞1，且x≠2时，$\frac{{ln（{x-1}）}}{x-2}＞\frac{a}{x}$恒成立，求实数a的范围．
15．下列说法中错误的有③④．
①已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x-2}，x≥0}\\{{2}^{-x}，x＜0}\end{array}\right.$，则f[f（-2）]=4；
②已知O为平面内任意一点，A，B，C是平面内互不相同的三点，且满足$\overrightarrow{OA}=x\overrightarrow{OB}+y\overrightarrow{OC}$，x+y=1，则A，B，C三点共线；
③已知平面α∩平面β=l，直线a?α且a⊥直线l，直线b?β，则a⊥b是α⊥β的充要条件；
④若△ABC是锐角三角形，则cosA＜cosB；
⑤若f（x）=sin（2x+φ）-cos（2x-φ）的最大值为1，且φ∈（0，$\frac{π}{2}$），则f（x）的单调增区间为[kπ-$\frac{π}{8}$，kπ+$\frac{3π}{8}$]（k∈Z）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网