题目内容
函数y=f(x)(x≠0)是奇函数,且当x∈(0,+∞)时为增函数,且f(1)=0。
(1)求关于t的方程f(2t+5)=0的解;
(2)求不等式f[x(x-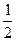 )]<0的解集。
)]<0的解集。
(1)求关于t的方程f(2t+5)=0的解;
(2)求不等式f[x(x-
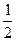 )]<0的解集。
)]<0的解集。(1) t= -2或t= -3
(2)
(2)

(1)由奇函数性质可知f(-1)= -f(1)=0,
∴2t+5=1或2t+5=" -1"
∴t= -2或t= -3
(2)∵当x∈(0,+∞)时为增函数,所以当x∈(-∞,0)时也为增函数。
故0<t<1时f(t)<f(1), t< -1时 f(t)<f( -1)
t>1时f(t)>f(1), -1<t<0 时 f(t)>f(-1)
可知f(t)<0的解集为{t|t<-1或0<t<1}
所以f[x(x-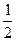 )]<0的解集为{x|x(x-
)]<0的解集为{x|x(x-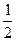 )<-1或0<x(x-
)<-1或0<x(x-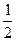 )<1}
)<1}
即
∴2t+5=1或2t+5=" -1"
∴t= -2或t= -3
(2)∵当x∈(0,+∞)时为增函数,所以当x∈(-∞,0)时也为增函数。
故0<t<1时f(t)<f(1), t< -1时 f(t)<f( -1)
t>1时f(t)>f(1), -1<t<0 时 f(t)>f(-1)
可知f(t)<0的解集为{t|t<-1或0<t<1}
所以f[x(x-
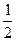 )]<0的解集为{x|x(x-
)]<0的解集为{x|x(x-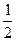 )<-1或0<x(x-
)<-1或0<x(x-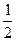 )<1}
)<1}即


练习册系列答案
相关题目
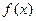 是定义在
是定义在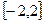 上的奇函数,当
上的奇函数,当 时,
时,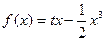 (
(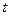 为常数)。
为常数)。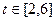 时,求
时,求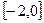 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的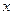 ,并猜想
,并猜想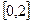 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);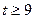 时,证明:函数
时,证明:函数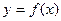 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线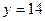 上。
上。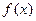 是奇函数,则
是奇函数,则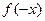 是奇函数”的否定是
是奇函数”的否定是 
 若函数
若函数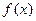 在其定义域上有且仅有四个不同的零点,则实数a的取值范围是 。
在其定义域上有且仅有四个不同的零点,则实数a的取值范围是 。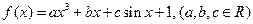 若
若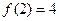 ,则
,则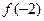 = .
= .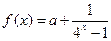 ,若
,若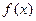 为奇函数,则
为奇函数,则 ▲
▲ 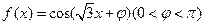 ,若
,若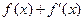 为奇函数,则
为奇函数,则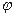 =_____;
=_____;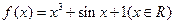 ,若
,若
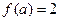 ,则
,则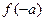 的值为( )
的值为( ) -1
-1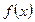 是定义在R上的奇函数,又
是定义在R上的奇函数,又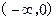 是增函数,且
是增函数,且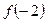 =0,则满足
=0,则满足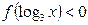 的
的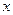 的取值范围为
的取值范围为 