题目内容
在直角坐标系中,若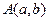 ,
,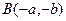 在函数
在函数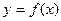 的图像上,称
的图像上,称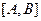 为函数
为函数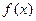 的一组关于原点的中心对称点,
的一组关于原点的中心对称点,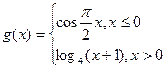 关于原点的中心对称点有多少组
关于原点的中心对称点有多少组
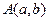 ,
,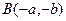 在函数
在函数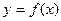 的图像上,称
的图像上,称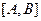 为函数
为函数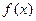 的一组关于原点的中心对称点,
的一组关于原点的中心对称点,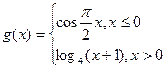 关于原点的中心对称点有多少组
关于原点的中心对称点有多少组2
不妨设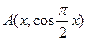 ,则
,则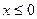 ,所以
,所以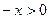 ,故
,故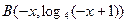
从而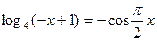
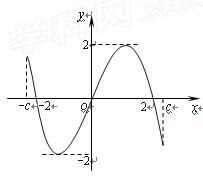
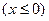 ,由图可知两函数图像在
,由图可知两函数图像在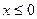 只有两个
只有两个
交点故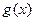 关于原点的中心对称点有
关于原点的中心对称点有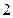 组
组
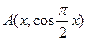 ,则
,则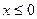 ,所以
,所以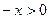 ,故
,故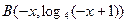
从而
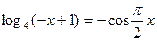
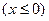 ,由图可知两函数图像在
,由图可知两函数图像在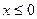 只有两个
只有两个交点故
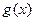 关于原点的中心对称点有
关于原点的中心对称点有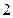 组
组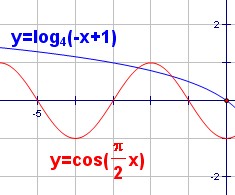 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
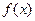 是定义在
是定义在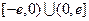 上的奇函数,当
上的奇函数,当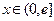 时
时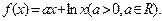
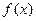 的解析式;
的解析式;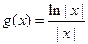 ,
,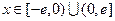 ,求证:当
,求证:当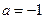 时,
时,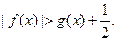
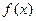 是定义在
是定义在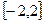 上的奇函数,当
上的奇函数,当 时,
时,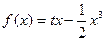 (
(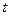 为常数)。
为常数)。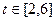 时,求
时,求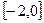 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的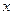 ,并猜想
,并猜想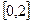 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);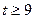 时,证明:函数
时,证明:函数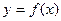 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线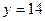 上。
上。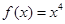 ;(2)
;(2)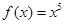 ,(3)
,(3)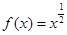 ,(4)
,(4)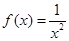 中是奇函数的有( )
中是奇函数的有( )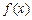 是定义在
是定义在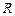 上的奇函数,当
上的奇函数,当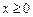 时,
时,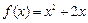 ,若
,若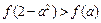 ,则实数
,则实数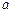 的取值范围是( )
的取值范围是( )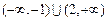
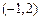
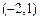
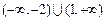
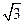 ),N (4,
),N (4,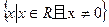 又f(x)在
又f(x)在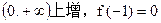 ,则f(x)>0的解集是( )
,则f(x)>0的解集是( )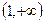 B (0,1) C
B (0,1) C 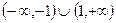 D
D 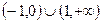
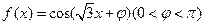 ,若
,若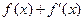 为奇函数,则
为奇函数,则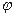 =_____;
=_____;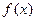 是定义在区间
是定义在区间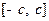 (
(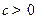 )上的奇函数,令
)上的奇函数,令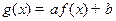 ,并有关于函数
,并有关于函数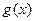 的四个论断:
的四个论断: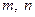 (
(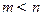 ),
),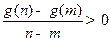 恒成立;
恒成立;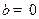 ,则函数
,则函数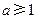 ,
,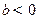 ,则方程
,则方程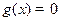 必有3个实数根;
必有3个实数根;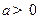 ,则
,则