题目内容
12.如图是函数f(x)=x3+bx2+cx+d的大致图象,则x1+x2=( )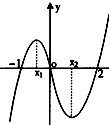
| A. | $\frac{2}{3}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |
分析 解:由图象知f(-1)=f(0)=f(2)=0,解出 b、c、d的值,由x1和x2是f′(x)=0的根,使用根与系数的关系得到x1+x2=$\frac{2}{3}$.
解答 解:∵f(x)=x3+bx2+cx+d,由图象知,-1+b-c+d=0,0+0+0+d=0,
8+4b+2c+d=0,∴d=0,b=-1,c=-2
∴f′(x)=3x2+2bx+c=3x2-2x-2. 由题意有x1和x2是函数f(x)的极值,
故有x1和x2是f′(x)=0的根,∴x1+x2=$\frac{2}{3}$,
故选:A.
点评 本题考查一元二次方程根的分布,根与系数的关系,函数在某点取的极值的条件,以及求函数的导数,属中档题

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
20.甲、乙、丙三人到三个景点旅游,每人只去一个景点,设事件A为“三个人去的景点不相同”,事件B为“甲独自去一个景点”,则概率P(A|B)等于( )
| A. | $\frac{4}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
4.等差数列{an}的前n项和为Sn,如果存在正整数k和l(k≠l),使得Sk=kl2,Sl=lk2,则( )
| A. | Sk+1的最小值为-6 | B. | Sk+l的最大值为-6 | ||
| C. | Sk+1的最小值为6 | D. | Sk+l的最小值为6 |
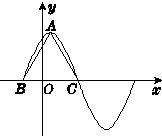 函数f(x)=3cosωx+$\sqrt{3}$sinωx(ω>0)在一个周期内的图象如图所示,A为图象的最高点.B、C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=3cosωx+$\sqrt{3}$sinωx(ω>0)在一个周期内的图象如图所示,A为图象的最高点.B、C为图象与x轴的交点,且△ABC为正三角形.