题目内容
18.已知圆C:x2+y2=2,点A(-2,0)及点B(3,a),从A点观察B点,若视线被圆C挡住,则a的取值范围是(5,+∞)∪(-∞,-5).分析 先设过A的直线方程为:kx-y+2k=0,根据“使视线不被圆C挡住”则找到直线与圆相切的位置,这样,先求得圆心到直线的距离,再让其等于半径,求得切线方程,再令x=4得y=±5,从而求得实数a的取值范围.
解答 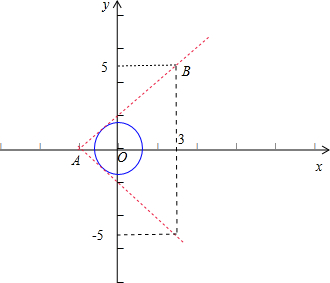 解:已知圆C:x2 +y2 =2,表示以(0,0)为圆心、半径等于$\sqrt{2}$的圆,
解:已知圆C:x2 +y2 =2,表示以(0,0)为圆心、半径等于$\sqrt{2}$的圆,
又点A(-2,0)及点B(3,a),
设过A的圆的切线方程为:kx-y+2k=0,根据圆心(0,0)到直线的距离 d=$\frac{|0-0+2k|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$.
解得k=±1,故圆的过点A(-2,0)的切线方程为 y=±(x+2).
再把x=3代入圆的切线方程求得y=±5,
故要使视线不被圆C挡住,则实数a的取值范围是 (5,+∞)∪(-∞,-5),
故答案为:(5,+∞)∪(-∞,-5).
点评 本题主要考查直线与圆的位置关系,作为相切是研究相交和相离的关键位置,应熟练掌握,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
8.已知某校5个学生的数学成绩和物理成绩如下表:
(1)通过大量事实证明发现,一个学生的数学成绩和物理成绩是具有很强的线性相关关系,用x表示数学成绩,用y表示物理成绩,求y关于x的回归方程;
(2)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”?
参考公式:残差和公式为:$\sum_{i=1}^{5}$(${y}_{i}-\widehat{{y}_{i}}$)).
| 学生的编号 | 1 | 2 | 3 | 4 | 5 |
| 数学成绩xi | 80 | 75 | 70 | 65 | 60 |
| 物理成绩yi | 70 | 66 | 68 | 64 | 62 |
(2)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”?
参考公式:残差和公式为:$\sum_{i=1}^{5}$(${y}_{i}-\widehat{{y}_{i}}$)).
8.已知sin(3π+α)=$\frac{1}{3}$,则cos2α等于( )
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
 如图,棱锥的底ABCD是一个矩形,AC与BD交于M,VM是棱锥的高,若VM=4cm,AB=4cm,VC=5cm,求棱锥的体积.
如图,棱锥的底ABCD是一个矩形,AC与BD交于M,VM是棱锥的高,若VM=4cm,AB=4cm,VC=5cm,求棱锥的体积. 正方体ABCD-A1B1C1D1中,E,F分别是BC,C1D1的中点.
正方体ABCD-A1B1C1D1中,E,F分别是BC,C1D1的中点.