题目内容
【题目】对于定义域相同的函数![]() 和
和![]() ,若存在实数
,若存在实数![]() ,
,![]() 使
使![]() ,则称函数
,则称函数![]() 是由“基函数
是由“基函数![]() ,
,![]() ”生成的.
”生成的.
(1)若函数![]() 是“基函数
是“基函数![]() ,
,![]() ”生成的,求实数
”生成的,求实数![]() 的值;
的值;
(2)试利用“基函数![]() ,
,![]() ”生成一个函数
”生成一个函数![]() ,且同时满足:①
,且同时满足:①![]() 是偶函数;②
是偶函数;②![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .求函数
.求函数![]() 的解析式.
的解析式.
【答案】(1) ![]() . (2)
. (2) ![]()
【解析】
(1)根据基函数的定义列方程,比较系数后求得![]() 的值.(2)设出
的值.(2)设出![]() 的表达式,利用
的表达式,利用![]() 为偶函数,结合偶函数的定义列方程,化简求得
为偶函数,结合偶函数的定义列方程,化简求得![]() ,由此化简
,由此化简![]() 的表达式
的表达式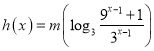 ,构造函数
,构造函数![]() ,利用定义法证得
,利用定义法证得![]() 在
在![]() 上的单调性,由此求得
上的单调性,由此求得![]() 的最小值,也即
的最小值,也即![]() 的最小值,从而求得
的最小值,从而求得![]() 的最小值,结合题目所给条件,求出
的最小值,结合题目所给条件,求出![]() 的值,即求得
的值,即求得![]() 的解析式.
的解析式.
解:(1)由已知得![]() ,
,
即![]() ,
,
得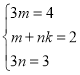 ,所以
,所以![]() .
.
(2)设![]() ,则
,则![]() .
.
由![]() ,得
,得![]() ,
,
整理得 ,即
,即![]() ,
,
即![]() 对任意
对任意![]() 恒成立,所以
恒成立,所以![]() .
.
所以![]()
![]()
![]()
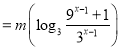 .
.
设![]() ,
,![]() ,令
,令![]() ,则
,则![]() ,
,
任取![]() ,且
,且![]()
则![]()
![]() ,
,
因为![]() ,且
,且![]()
所以![]() ,
,![]() ,
,![]() ,故
,故![]()
即![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,且当
,且当![]() 时取到“
时取到“![]() ”.
”.
所以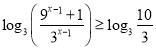 ,
,
又![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,
,
所以![]() ,且
,且![]() ,此时,
,此时,![]()
所以![]()

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目