题目内容
设 是把坐标平面上的点的横坐标伸长为原来的4倍,纵坐标伸长为原来的3倍的伸压变换,则圆
是把坐标平面上的点的横坐标伸长为原来的4倍,纵坐标伸长为原来的3倍的伸压变换,则圆 在
在 的作用下的新曲线的方程是
的作用下的新曲线的方程是
 是把坐标平面上的点的横坐标伸长为原来的4倍,纵坐标伸长为原来的3倍的伸压变换,则圆
是把坐标平面上的点的横坐标伸长为原来的4倍,纵坐标伸长为原来的3倍的伸压变换,则圆 在
在 的作用下的新曲线的方程是
的作用下的新曲线的方程是 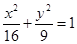
解:解:∵矩阵M对应的变换是把坐标平面上的点的横坐标伸长3倍,再将纵坐标伸长2倍的两个伸压变换的复合,
∴逆矩阵M-1是把坐标平面上的点的纵坐标缩短到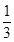 倍,横坐标缩短到
倍,横坐标缩短到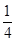 倍的伸压变换,
倍的伸压变换,
∴M-1=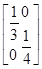 .(5分)
.(5分)
任意选取椭圆 x2+y2=1上的一点P(x0,y0),它在矩阵 M-1=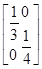 对应的变换下变为P'(x0′,y0′),则有
对应的变换下变为P'(x0′,y0′),则有 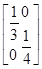
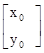 =
= 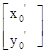 ,故
,故
x0="2x" ′0
y0="3y" ′0 .
又因为点P在椭圆 x2+y2=1上,所以9x0'2+16y0'2=1.
椭圆 x2+y2=1在M-1的作用下的新曲线的方程为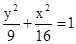
∴逆矩阵M-1是把坐标平面上的点的纵坐标缩短到
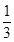 倍,横坐标缩短到
倍,横坐标缩短到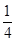 倍的伸压变换,
倍的伸压变换,∴M-1=
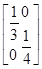 .(5分)
.(5分)任意选取椭圆 x2+y2=1上的一点P(x0,y0),它在矩阵 M-1=
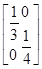 对应的变换下变为P'(x0′,y0′),则有
对应的变换下变为P'(x0′,y0′),则有 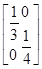
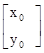 =
= 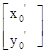 ,故
,故 x0="2x" ′0
y0="3y" ′0 .
又因为点P在椭圆 x2+y2=1上,所以9x0'2+16y0'2=1.
椭圆 x2+y2=1在M-1的作用下的新曲线的方程为
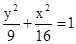

练习册系列答案
相关题目
 的离心率为
的离心率为 ,并且直线
,并且直线 是抛物线
是抛物线 的一条切线。
的一条切线。 的动直线
的动直线 交椭圆
交椭圆 于
于 、
、 两点,试问:在直角坐标平面上是否存在一个定点
两点,试问:在直角坐标平面上是否存在一个定点 ,使得以
,使得以 为直径的圆恒过点
为直径的圆恒过点 离心率为
离心率为 ,且过点
,且过点 .
. 椭圆
椭圆
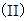 已知
已知
 直线
直线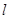 与椭圆
与椭圆 交于A、B两点,与
交于A、B两点,与 轴交于
轴交于 点,若
点,若 ,
, ,
, 的标准方程。
的标准方程。
 的距离之和等于4,设点P的轨迹为C。
的距离之和等于4,设点P的轨迹为C。 与C交于A、B两点,k为何值时
与C交于A、B两点,k为何值时 ?
? 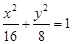 两焦点
两焦点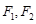 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点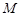 ,使得△
,使得△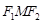 为直角三角形;
为直角三角形;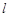 过抛物线
过抛物线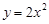 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于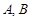 两点,则
两点,则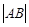 的最小值为2;
的最小值为2;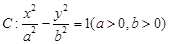 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为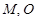 为坐标原点,则
为坐标原点,则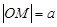 ;
; ,
,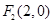 ,曲线
,曲线 上的动点
上的动点 满足
满足 ,直线
,直线 与曲线
与曲线 .
. ,若
,若
 ,求直线
,求直线 的方程.
的方程. 和
和 ,又过点
,又过点 .
. 在这个椭圆上,且
在这个椭圆上,且 ,求
,求 的余弦的大小.
的余弦的大小. 中,满足
中,满足 ,
, .若一个椭圆恰好以
.若一个椭圆恰好以 为一个焦点,另一个焦点在线段
为一个焦点,另一个焦点在线段 上,且
上,且 ,
, 均在此椭圆上,则该椭圆的离心率为 .
均在此椭圆上,则该椭圆的离心率为 . 的离心率为
的离心率为 ,且过点Q(1,
,且过点Q(1,
 (O为坐标原点),求实数t的最小值.
(O为坐标原点),求实数t的最小值.