题目内容
4.设数列{an}的通项公式为an=3n(n∈N*).数列{bn}定义如下:对任意m∈N*,bm是数列{an}中不大于32m的项的个数,则b3=243;数列{bm}的前m项和Sm=$\frac{3}{8}({9^m}-1)$.分析 利用数列{bn}定义如下:对任意m∈N*,bm是数列{an}中不大于32m的项的个数,可得bm=32m-1,即可得出结论.
解答 解:由题意,3n≤36,∴n≤243,∴b3=243;
由3n≤32m,∴n≤32m-1,∴bm=32m-1,∴Sm=$\frac{3(1-{9}^{m})}{1-9}$=$\frac{3}{8}({9^m}-1)$.
故答案为:243,$\frac{3}{8}({9^m}-1)$.
点评 本题考查等比数列的性质与求和,考查学生的计算能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.如图可表示函数y=f(x)图象的是( )
| A. | 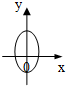 | B. | 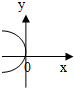 | C. | 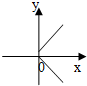 | D. | 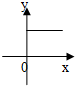 |
16.在一段线路中并联着两个独立自动控制的开关,只要其中一个开关能够闭合,线路就可以正常工作.设这两个开关能够闭合的概率分别为0.5和0.7,则线路能够正常工作的概率是( )
| A. | 0.35 | B. | 0.65 | C. | 0.85 | D. | $\frac{5}{7}$ |
13.已知f(x)=ax,g(x)=logax,h(x)=xa,若0<a<1,则f(2),g(2),h(2)的大小关系是( )
| A. | f(2)>g(2)>h(2) | B. | g(2)>f(2)>h(2) | C. | h(2)>g(2)>f(2) | D. | h(2)>f(2)>g(2) |
6.下列说法正确的是( )
| A. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | |
| B. | 函数f(x)=ex-2的零点落在区间(0,1)内 | |
| C. | 函数f(x)=x+$\frac{1}{x}$的最小值为2 | |
| D. | 若m=4,则直线2x+my+1=0与直线mx+8y+2=0互相平行 |
 在长方体ABCD-A1B1C1D1中,E为DD1的中点.
在长方体ABCD-A1B1C1D1中,E为DD1的中点.