题目内容
已知OA是球O的半径，过点A作与直线OA成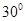
的平面截球面得到圆M，若圆M的面积为15
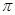，则球O的表面积是
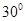的平面截球面得到圆M，若圆M的面积为15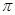，则球O的表面积是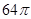 
解：解：设球半径为R，圆C的半径为r，
由πr2=15π，得r2=15．
由题意可得：OC="1/" 2 •R/ 2 ="1" 4 R．
所以 R2="(1" /4 R)2+r2="1" 16 R2+15，
解得R2=16
所以球O的表面积为64π．
故答案为：64π
由πr2=15π，得r2=15．
由题意可得：OC="1/" 2 •R/ 2 ="1" 4 R．
所以 R2="(1" /4 R)2+r2="1" 16 R2+15，
解得R2=16
所以球O的表面积为64π．
故答案为：64π
练习册系列答案
相关题目
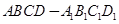是底面边长为1的正四棱柱，
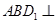平面
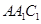
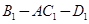的平面角为120°时，求四棱锥
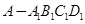的体积。
.
.
.
.
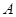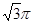
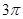
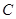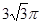
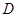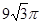
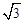正方形。若PA=2
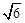，则△OAB的面积为______________.
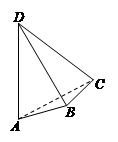
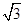．则正三棱锥S - ABC的外接球的体积为 。
，一个球内切于该正方体，那么这个球的体积是（ ）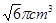
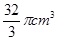
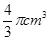
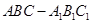的侧棱与底面边长都相等且为1，
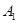在底面
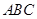内的射影为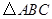
的中心，则三棱柱