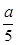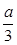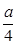题目内容
正三棱锥S-ABC中,M、N分别是SC.BC中点,且MN⊥AM,若SA=2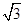 .则正三棱锥S - ABC的外接球的体积为 。
.则正三棱锥S - ABC的外接球的体积为 。
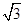 .则正三棱锥S - ABC的外接球的体积为 。
.则正三棱锥S - ABC的外接球的体积为 。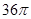
∵三棱锥S-ABC正棱锥,∴SB⊥AC(对棱互相垂直)∴MN⊥AC
又∵MN⊥AM而AM∩AC=A,∴MN⊥平面SAC即SB⊥平面SAC
∴∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球
∴2R=23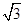 •
•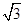 ,∴R=3,∴S=4πR2=4π•(3)2=36π
,∴R=3,∴S=4πR2=4π•(3)2=36π
又∵MN⊥AM而AM∩AC=A,∴MN⊥平面SAC即SB⊥平面SAC
∴∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球
∴2R=23
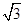 •
•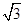 ,∴R=3,∴S=4πR2=4π•(3)2=36π
,∴R=3,∴S=4πR2=4π•(3)2=36π
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
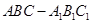 中,
中,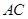 ⊥
⊥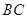 ,
,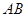 ⊥
⊥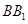 ,
,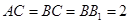 ,
,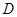 为
为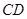 ⊥
⊥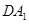 .
.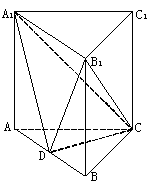
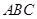 ;(2)求三棱锥
;(2)求三棱锥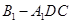 的体积.
的体积.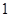 的球内切于一个底面半径为
的球内切于一个底面半径为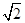 的圆锥。
的圆锥。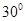 的平面截球面得到圆M,若圆M的面积为15
的平面截球面得到圆M,若圆M的面积为15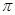 ,则球O的表面积是
,则球O的表面积是 
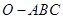 中,三条棱
中,三条棱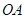 ,
,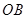 ,
,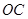 两两垂直,且
两两垂直,且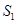 ,
,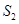 ,
,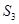 ,则
,则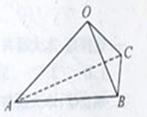
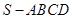 中,
中,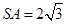 ,那么当该棱锥的体积最大时,它的高为
,那么当该棱锥的体积最大时,它的高为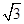
 ,它的表面积为
,它的表面积为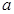 ,则它的底面积为( ).
,则它的底面积为( ).