题目内容
设函数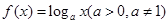 ,已知数列
,已知数列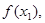
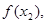
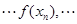 是公差为2的等差数列,且
是公差为2的等差数列,且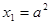 .
.
(Ⅰ)求数列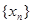 的通项公式;
的通项公式;
(Ⅱ)当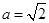 时,求数列
时,求数列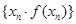 的前
的前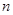 项和
项和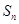 .
.
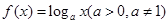 ,已知数列
,已知数列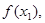
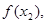
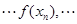 是公差为2的等差数列,且
是公差为2的等差数列,且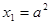 .
.(Ⅰ)求数列
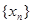 的通项公式;
的通项公式; (Ⅱ)当
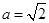 时,求数列
时,求数列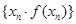 的前
的前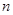 项和
项和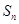 .
.(Ⅰ) .(Ⅱ)
.(Ⅱ) .
.
 .(Ⅱ)
.(Ⅱ) .
. 试题分析:(Ⅰ)
 ,且
,且 ,
, ,即
,即 ,
,所以
 . 6分
. 6分(Ⅱ)当
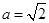 时,
时, ,
,则
 , 8分
, 8分两式相减得
 , 11分
, 11分所以
 . 12分
. 12分点评:中档题,本题综合考查、等比数列的基础知识,对数函数的性质,本解答从确定通项公式入手,明确了所研究数列的特征。“分组求和法”、“错位相消法”、“裂项相消法”是高考常常考到数列求和方法。

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
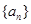 的前
的前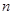 项和为
项和为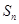 ,且
,且 ,
,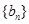 满足
满足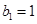 ,且点
,且点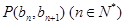 在直线
在直线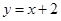 上.
上.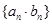 的前
的前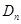 ;
;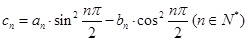 ,求数列
,求数列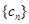 的前
的前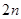 项和
项和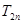 .
.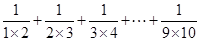 得( )
得( )
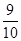
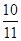
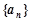 是有穷数列,且项数
是有穷数列,且项数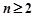 .定义一个变换
.定义一个变换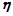 :将数列
:将数列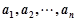 ,变成
,变成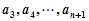 ,其中
,其中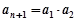 是变换所产生的一项.从数列
是变换所产生的一项.从数列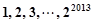 开始,反复实施变换
开始,反复实施变换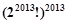
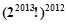
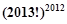
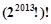
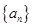 的前n项和为
的前n项和为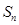 ,且满足
,且满足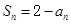 ,n=1,2,3,…….
,n=1,2,3,…….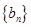 满足
满足 ,且
,且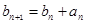 ,求数列
,求数列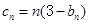 ,求数列
,求数列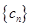 的前n项和
的前n项和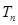 .
. 中,
中, ,
, 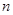 项和
项和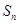
 的各项均为正数,
的各项均为正数,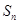 为其前
为其前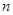 项和,且对任意的
项和,且对任意的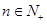 ,有
,有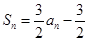 .
. ,求数列
,求数列 的前
的前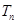 .
. 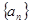 的通项公式
的通项公式 .若数列
.若数列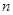 项和
项和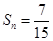 ,则
,则