题目内容
已知数列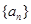 的前
的前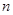 项和为
项和为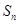 ,且
,且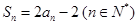 ,
,
数列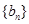 满足
满足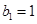 ,且点
,且点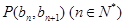 在直线
在直线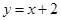 上.
上.
(Ⅰ)求数列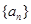 、
、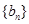 的通项公式;
的通项公式;
(Ⅱ)求数列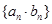 的前
的前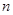 项和
项和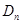 ;
;
(Ⅲ)设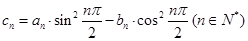 ,求数列
,求数列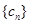 的前
的前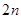 项和
项和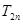 .
.
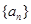 的前
的前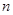 项和为
项和为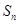 ,且
,且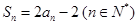 ,
,数列
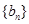 满足
满足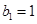 ,且点
,且点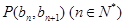 在直线
在直线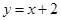 上.
上.(Ⅰ)求数列
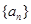 、
、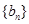 的通项公式;
的通项公式;(Ⅱ)求数列
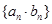 的前
的前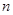 项和
项和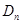 ;
;(Ⅲ)设
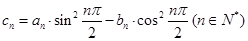 ,求数列
,求数列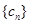 的前
的前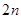 项和
项和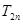 .
.(Ⅰ)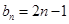 (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ)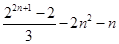
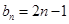 (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ)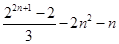
试题分析:解:(Ⅰ)当
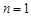 ,
,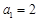 ;当
;当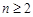 时,
时,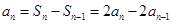
∴
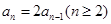 ,∴
,∴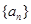 是等比数列,公比为2,首项
是等比数列,公比为2,首项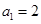 ∴
∴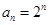
又点
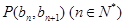 在直线
在直线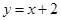 上,∴
上,∴ 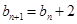 ,
,∴
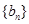 是等差数列,公差为2,首项
是等差数列,公差为2,首项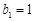 ,∴
,∴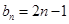
(Ⅱ)∴
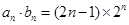
∴
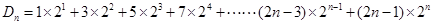 ①
①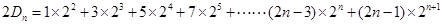 ②
②①—②得
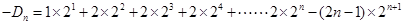


(Ⅲ)
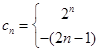
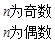
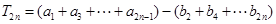
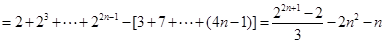 .
.点评:对于求一般数列的通项公式或前n项和时,常用方法有:错位相减法、裂变法等,目的是消去中间部分,本题就用到错位相减法。

练习册系列答案
相关题目
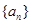 的前n项和为
的前n项和为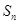 ,已知
,已知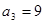 ,
, 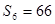 .
.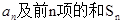 ;
;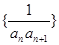 的前n项和为
的前n项和为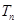 ,证明:
,证明: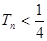 ;
;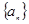 的前
的前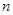 项和为
项和为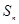 ,
,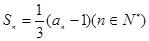
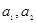 ;
;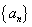 中,
中, 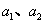 是正整数,且
是正整数,且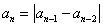 ,
,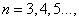 则称数列
则称数列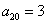 ,
,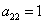 ,则
,则 .
.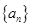 中,
中,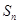 是其前
是其前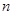 项和,若
项和,若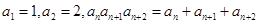 ,且
,且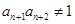 ,则
,则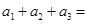 ________,
________,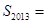 ______;
______;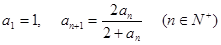 ,试猜想这个数列的通项公式。
,试猜想这个数列的通项公式。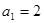 ,当
,当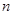 为奇数时,
为奇数时,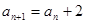 ;当
;当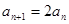 ;则
;则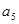 等于 .
等于 .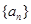 的前n项和为
的前n项和为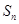 ,令
,令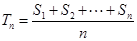 ,称
,称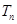 为数列
为数列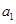 ,
,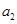 , ,
, ,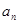 的“理想数”,已知数列
的“理想数”,已知数列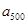 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 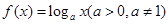 ,已知数列
,已知数列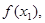
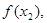
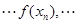 是公差为2的等差数列,且
是公差为2的等差数列,且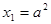 .
.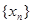 的通项公式;
的通项公式; 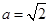 时,求数列
时,求数列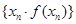 的前
的前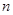 项和
项和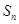 .
.