题目内容
已知数列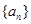 的各项均为正数,
的各项均为正数,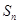 为其前
为其前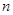 项和,且对任意的
项和,且对任意的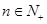 ,有
,有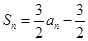 .
.
(1)求数列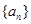 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列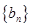 的前
的前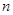 项和
项和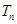 .
.
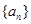 的各项均为正数,
的各项均为正数,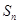 为其前
为其前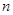 项和,且对任意的
项和,且对任意的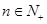 ,有
,有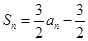 .
.(1)求数列
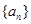 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列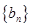 的前
的前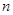 项和
项和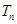 .
. (1)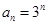 (2)
(2)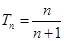
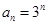 (2)
(2)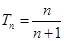
试题分析:(1)由已知得
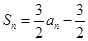 ,
,∴当
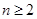 时,
时,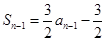 ;
; ∴
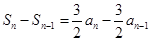 ,即
,即 ,
,∴当
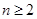 时,
时,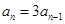 ;
;∴数列
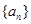 为等比数列,且公比
为等比数列,且公比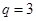 ; ……4分
; ……4分又当
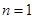 时,
时,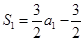 ,即
,即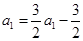 ,∴
,∴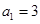 ;
;∴
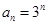 . ……8分
. ……8分(2)∵
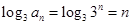 ,
,∴
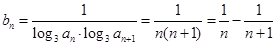 , ……10分
, ……10分∴
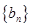 的前
的前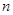 项和
项和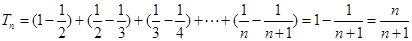 . ……12分
. ……12分点评:判定等差数列或等比数列时,不要忘记验证
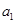 是否符合;裂项法是求和的主要方法之一,要正确裂项,准确计算.
是否符合;裂项法是求和的主要方法之一,要正确裂项,准确计算.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
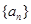 的前n项和为
的前n项和为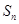 ,令
,令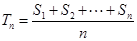 ,称
,称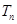 为数列
为数列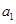 ,
,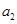 , ,
, ,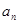 的“理想数”,已知数列
的“理想数”,已知数列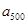 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 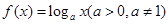 ,已知数列
,已知数列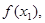
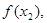
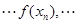 是公差为2的等差数列,且
是公差为2的等差数列,且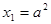 .
.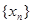 的通项公式;
的通项公式; 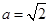 时,求数列
时,求数列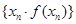 的前
的前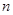 项和
项和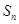 .
.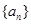 中,
中,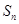 为其前
为其前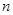 项和,满足
项和,满足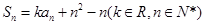 .
.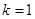 ,求数列
,求数列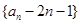 为公比不为1的等比数列,求
为公比不为1的等比数列,求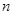 行的各数之和等于
行的各数之和等于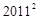 ,则
,则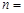
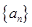 的通项公式是
的通项公式是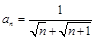 ,若前
,若前 项和为
项和为 ,则项数
,则项数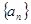 的各项均为正数,
的各项均为正数,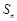 为其前
为其前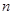 项和,对于任意
项和,对于任意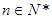 ,总有
,总有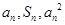 成等差数列.
成等差数列.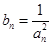 ,数列
,数列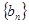 的前
的前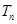 ,求证:
,求证: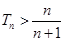 .
. 的前5项的和是 。
的前5项的和是 。 ,将函数
,将函数 的所有极值点从小到大排成一数列,记为
的所有极值点从小到大排成一数列,记为
 的通项公式;
的通项公式; ,求数列
,求数列 前n项和
前n项和