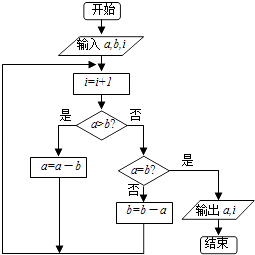
题目内容
【题目】已知函数f(x)=2sin( ![]() ﹣φ)(0<φ<
﹣φ)(0<φ< ![]() )的图象经过点(0,﹣1).
)的图象经过点(0,﹣1).
(1)求函数f(x)的对称轴方程及相邻两条对称轴间的距离d;
(2)设α、β∈[0, ![]() ],f(3α+
],f(3α+ ![]() )=
)= ![]() ,f(3β+2π)=
,f(3β+2π)= ![]() ,求cos(α+β)的值.
,求cos(α+β)的值.
【答案】
(1)解:函数f(x)=2sin( ![]() ﹣φ)的图象经过点(0,﹣1),
﹣φ)的图象经过点(0,﹣1),
∴2sin(﹣φ)=﹣1,∴sinφ= ![]() ;
;
又0<φ< ![]() ,
,
∴φ= ![]() ;
;
∴函数f(x)=2sin( ![]() ﹣
﹣ ![]() );
);
令 ![]() ﹣
﹣ ![]() =kπ+
=kπ+ ![]() ,k∈Z,
,k∈Z,
解得x=3kπ+2π,k∈Z,
∴f(x)图象的对称轴方程是x=3kπ+2π,k∈Z;
且相邻两条对称轴间的距离d=(3π+2π)﹣2π=3π
(2)解:由α、β∈[0, ![]() ],f(3α+
],f(3α+ ![]() )=2sinα=
)=2sinα= ![]() ,
,
∴sinα= ![]() ,cosα=
,cosα= ![]() ;
;
f(3β+2π)=2sin(β+ ![]() )=2cosβ=
)=2cosβ= ![]() ,
,
∴cosβ= ![]() ,sinβ=
,sinβ= ![]() ;
;
∴cos(α+β)=cosαcosβ﹣sinαsinβ= ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]()
【解析】(1)根据题意求出函数f(x)的解析式,利用正弦函数的图象性质求出f(x)图象的对称轴方程以及相邻两条对称轴间的距离d;(2)由题意求出sinα、cosα和cosβ、sinβ的值,再计算cos(α+β)的值.

 阅读快车系列答案
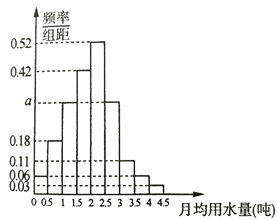
阅读快车系列答案【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问部分职工,根据被访问职工对该部门的评分,绘制频率分布直方图(如图所示).
(1)求频率分布表中①、②、③位置相应数据,并在答题纸上完成频率分布直方图;
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.050 |
第2组 | [60,70) | ① | 0.350 |
第3组 | [70,80) | 30 | ② |
第4组 | [80,90) | 20 | 0.200 |
第5组 | [90,100] | 10 | 0.100 |
合计 | ③ | 1.00 | |
(2)为进一步了解情况,该企业决定在第3,4,5组中用分层抽样抽取5名职工进行座谈,求第3,4,5组中各自抽取的人数;
(3)求该样本平均数 ![]() .
.