题目内容
(本小题满分15分)
(Ⅰ)如图1, 是平面内的三个点,且
是平面内的三个点,且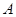 与
与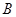 不重合,
不重合,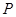 是平面内任意一点,若点
是平面内任意一点,若点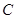 在直线
在直线 上,试证明:存在实数
上,试证明:存在实数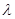 ,使得:
,使得: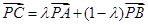 .
.
(Ⅱ)如图2,设 为
为 的重心,
的重心,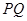 过
过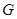 点且与
点且与 、
、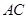 (或其延长线)分别交于
(或其延长线)分别交于 点,若
点,若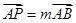 ,
,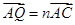 ,试探究:
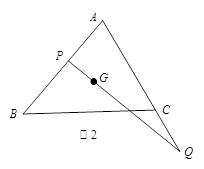
,试探究: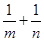 的值是否为定值,若为定值,求出这个定值;若不是定值,请说明理由.
的值是否为定值,若为定值,求出这个定值;若不是定值,请说明理由.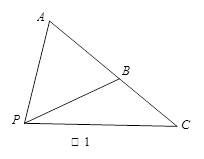
(Ⅰ)如图1,
 是平面内的三个点,且
是平面内的三个点,且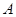 与
与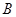 不重合,
不重合,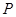 是平面内任意一点,若点
是平面内任意一点,若点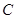 在直线
在直线 上,试证明:存在实数
上,试证明:存在实数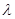 ,使得:
,使得: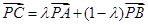 .
.(Ⅱ)如图2,设
 为
为 的重心,
的重心,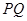 过
过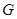 点且与
点且与 、
、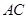 (或其延长线)分别交于
(或其延长线)分别交于 点,若
点,若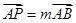 ,
,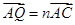 ,试探究:
,试探究: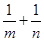 的值是否为定值,若为定值,求出这个定值;若不是定值,请说明理由.
的值是否为定值,若为定值,求出这个定值;若不是定值,请说明理由.

解:(Ⅰ)见解析;(Ⅱ)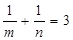 为定值.
为定值.
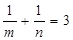 为定值.
为定值. 点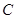 在直线
在直线 上,则点A,B,C共线,考查向量共线定理,
上,则点A,B,C共线,考查向量共线定理, ,将所有向量用P起始点,得出:
,将所有向量用P起始点,得出:
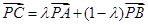 ;
;
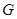 为
为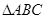 的重心
的重心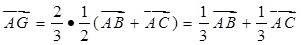 ,
,
分别得出向量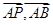 ,及向量
,及向量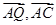 的关系。
的关系。
解:(Ⅰ)由于 三点共线,所以存在实数
三点共线,所以存在实数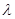 使得:
使得:
 , ………3分
, ………3分
即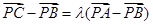 ………5分
………5分
化简为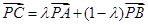
结论得证. ………7分
(Ⅱ)连结 ,因为
,因为 为
为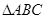 的重心,
的重心,
所以: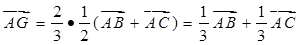 ………10分
………10分
又因为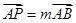 ,
,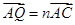
所以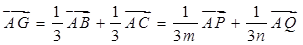 ………12分
………12分
由(Ⅰ)知: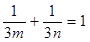 所以
所以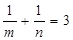 为定值.…15分
为定值.…15分
 在直线
在直线 上,则点A,B,C共线,考查向量共线定理,
上,则点A,B,C共线,考查向量共线定理, ,将所有向量用P起始点,得出:
,将所有向量用P起始点,得出: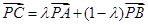 ;
; 为
为 的重心
的重心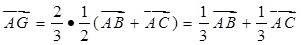 ,
,分别得出向量
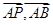 ,及向量
,及向量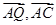 的关系。
的关系。解:(Ⅰ)由于
 三点共线,所以存在实数
三点共线,所以存在实数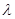 使得:
使得: , ………3分
, ………3分即
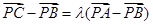 ………5分
………5分化简为
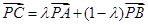
结论得证. ………7分
(Ⅱ)连结
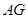 ,因为
,因为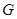 为
为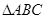 的重心,
的重心,所以:
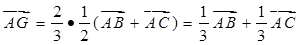 ………10分
………10分又因为
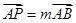 ,
,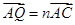
所以
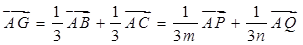 ………12分
………12分由(Ⅰ)知:
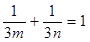 所以
所以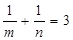 为定值.…15分
为定值.…15分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的重心,过G的直线
的重心,过G的直线 分别交AB,AC于
分别交AB,AC于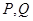 ,已知:
,已知: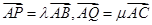 ,
,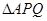 的面积分别为
的面积分别为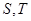 ,
,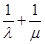 的值; (Ⅱ) 求
的值; (Ⅱ) 求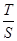 的取值范围.
的取值范围. 与
与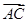 的夹角为
的夹角为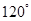 ,且
,且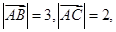 ,若,
,若,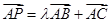 ,且
,且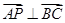 ,则实数
,则实数 的值为_____.
的值为_____.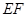 与平行四边形
与平行四边形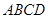 的两边
的两边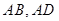 分别交于
分别交于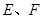 两点,且交其对角线于
两点,且交其对角线于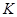 ,其中
,其中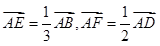 ,
,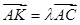 ,则
,则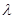 的值为 ( )
的值为 ( )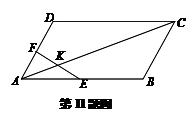



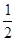
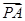 ,
,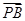 ,
,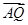 ,
,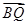 满足如下条件:
满足如下条件: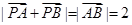 ;
;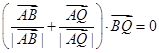 ;③
;③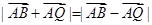 ,则
,则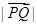 的最大值与最小值之差是( )
的最大值与最小值之差是( )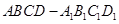 中,
中,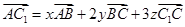 ,
,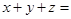 ( )
( )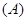 .1
.1 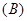 .
.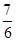
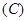 .
. 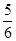
 .
.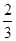
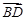 =
=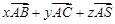 ,则x+y+z=
,则x+y+z=  中,
中, 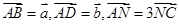 ,则
,则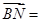 (用
(用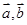 表示) ;
表示) ;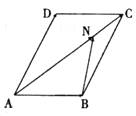
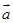 ,=
,=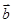 ,则=.(用
,则=.(用