题目内容
15.某班有34位同学,座位号记为01,02,…34,用下面的随机数表选取5组数作为参加青年志愿者活动的五位同学的座号.49 54 43 54 82 17 37 93 23 78 87 35 20
96 43 84 26 34 91 64 57 24 55 06 88 77
04 74 47 67 21 76 33 50 25 83 92 12 06
选取方法是从随机数表第一行的第6列和第7列数字开始,由左到右依次选取两个数字,则选出来的第4个志愿者的座号是 ( )
| A. | 23 | B. | 09 | C. | 02 | D. | 16 |
分析 利用随机数表法,按指定的顺序依次选两个数,不在01~34之内的去掉,由此得出5个样本数字.
解答 解:根据题意,利用随机数表法,
从随机数表第一行的第6列和第7列数字开始,由左向右依次选两个数,如下;
35(去掉),48(去掉),21(第1个),73(去掉),79(去掉),32(第2个),
37(去掉),88(去掉),73(去掉),52(去掉),09(第3个),64(去掉),
38(去掉),42(去掉),63(去掉),49(去掉),16(第4个),…;
所以,选出来的第4个志愿者的座号是16.
故选:D.
点评 本题考查了利用随机数表法进行样本数据的收集问题,是基础题目.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
3.已知命题p:“直线l垂直于平面α内的无数条直线”的充要条件是“l⊥α”;命题q:若平面α⊥平面β,直线a?β,则“a⊥α”是“a平行于β”的充分不必要条件,则正确命题是( )
| A. | p∧q | B. | (¬p)∧q | C. | (?p)∧(¬q) | D. | p∨(¬q) |
10.某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为ω.在区间[0,100]对企业没有造成经济损失;在区间∴F对企业造成经济损失成直线模型(当API为150时造成的经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
(1)试写出S(ω)的表达式:
(2)试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过900元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(b+c)(a+c)(b+d)}$
| API | [0.50] | (0,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)试写出S(ω)的表达式:
(2)试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过900元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
附:
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 | 100 |
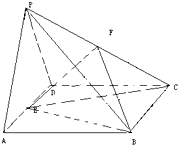 如图,△PAD为边长为2的等边三角形,ABCD为菱形,∠DAB=60°,E为AD的中点,平面PAD⊥平面ABCD,F为棱PC上一点,
如图,△PAD为边长为2的等边三角形,ABCD为菱形,∠DAB=60°,E为AD的中点,平面PAD⊥平面ABCD,F为棱PC上一点,