Question

5．如图，在平行六面体ABCD-A₁B₁C₁D₁中，AB=3，AD=4，AA₁=4，∠DAB=90°，∠BAA₁=∠DAA₁=60°，E是CC₁的中点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$．
（1）用$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$表示$\overrightarrow{AE}$；
（2）求|$\overrightarrow{AE}$|．

Answer 1

分析 （1）如图所示，∵$\overrightarrow{BC}=\overrightarrow{AD}$，$\overrightarrow{CE}=\frac{1}{2}\overrightarrow{C{C}_{1}}$=$\frac{1}{2}\overrightarrow{A{A}_{1}}$，利用向量的多边形法则可得$\overrightarrow{AE}$=$\overrightarrow{AB}+\overrightarrow{BC}$+$\overrightarrow{CE}$．
（2）利用向量数量积运算性质可得：$|\overrightarrow{AE}{|}^{2}$=$（\overrightarrow{a}+\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}）^{2}$=${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$+$\frac{1}{4}{\overrightarrow{c}}^{2}$+$2\overrightarrow{a}•\overrightarrow{b}$+$\overrightarrow{a}•\overrightarrow{c}$+$\overrightarrow{b}•\overrightarrow{c}$，代入即可得出．

解答 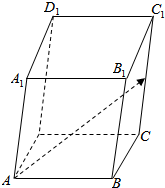解：（1）如图所示，∵$\overrightarrow{BC}=\overrightarrow{AD}$，$\overrightarrow{CE}=\frac{1}{2}\overrightarrow{C{C}_{1}}$=$\frac{1}{2}\overrightarrow{A{A}_{1}}$，
∴$\overrightarrow{AE}$=$\overrightarrow{AB}+\overrightarrow{BC}$+$\overrightarrow{CE}$=$\overrightarrow{a}+\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$．
（2）∵$|\overrightarrow{AE}{|}^{2}$=$（\overrightarrow{a}+\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}）^{2}$=${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$+$\frac{1}{4}{\overrightarrow{c}}^{2}$+$2\overrightarrow{a}•\overrightarrow{b}$+$\overrightarrow{a}•\overrightarrow{c}$+$\overrightarrow{b}•\overrightarrow{c}$=${3}^{2}+{4}^{2}+\frac{1}{4}×{4}^{2}$+0+$3×4×\frac{1}{2}$+$4×4×\frac{1}{2}$=43．
∴$|\overrightarrow{AE}|=\sqrt{43}$．

点评 本题考查了向量的多边形法则、向量数量积运算性质，考查了推理能力与计算能力．