题目内容
【题目】已知a、b、c为某一直角三角形的三条边长，c为斜边．若点（m，n）在直线ax+by+2c=0上，则m2+n2的最小值是 ．
【答案】4
【解析】试题分析：由直角三角形且c为斜边，根据勾股定理表示出一个关系式，因为所求式子即为原点到已知点距离的平方，而点到直线的距离只有垂线段最短，利用点到直线的距离公式表示出原点到已知直线的距离，把表示出的关系式代入即可求出原点到已知直线的距离，平方即可得到所求式子的最小值．
解：根据题意可知：当（m，n）运动到原点与已知直线作垂线的垂足位置时，m2+n2的值最小，
由三角形为直角三角形，且c为斜边，根据勾股定理得：c2=a2+b2，
所以原点（0，0）到直线ax+by+2c=0的距离d=
=2，
则m2+n2的最小值为4．
故答案为：4．
练习册系列答案
相关题目
【题目】某个体服装店经营某种服装,在某周内获得的纯利润y(单位:元)与该周每天销售这种服装的件数x之间的一组数据关系如下表:
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利润y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获得纯利润多少元?
已知:
=280,
xiyi=3 487,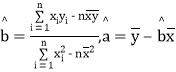
.
