题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() (
(![]() ,
,![]() )的右焦点
)的右焦点![]() ,且椭圆
,且椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
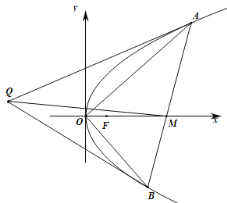
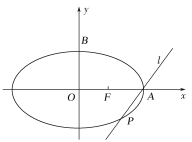
(2)设动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() ,且
,且![]() 的面积
的面积![]() .
.
①求证:![]() 为定值;
为定值;
②设直线![]() 的中点
的中点![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)①证明见解析;②
(2)①证明见解析;②![]() .
.
【解析】
(1)由题意可得![]() ,
,![]() ,求得
,求得![]() 后即可得解;
后即可得解;
(2)①当直线斜率不存在时易得![]() ,当直线斜率存在时,设直线方程为
,当直线斜率存在时,设直线方程为![]() ,可得
,可得![]() 、
、![]() 、
、![]() 、
、![]() ,由
,由![]() 可得
可得![]() ,再利用
,再利用![]() 化简即可得证;
化简即可得证;
②当直线的斜率不存在时,易得![]() ;当直线斜率存在时,设直线方程为
;当直线斜率存在时,设直线方程为![]() ,表示出
,表示出![]() 、
、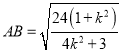 后,再利用基本不等式
后,再利用基本不等式![]() 化简即可得解.
化简即可得解.
(1)![]() 椭圆右焦点为
椭圆右焦点为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,
,
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,
![]() 椭圆方程为
椭圆方程为![]() .
.
(2)①证明:当直线![]() 斜率不存在时,设直线方程为
斜率不存在时,设直线方程为![]() ,则
,则![]() ,
,![]() ,
,
易知![]() ,
,![]()
![]() ,
,![]()
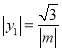 ,
,
![]()
![]() 解得
解得![]() ,此时
,此时![]() .
.
当直线![]() 斜率存在时,设直线方程为
斜率存在时,设直线方程为![]() ,
,
联立方程得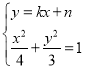 ,消去
,消去![]() 得
得![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
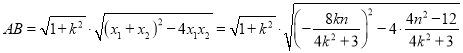
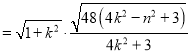 ,
,
又 原点![]() 到直线
到直线![]() 的距离
的距离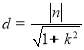 ,
,
![]()
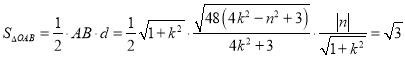 ,
,
化简得![]() ,解得
,解得![]() ,
,
![]()
![]()
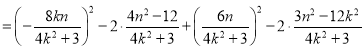
![]() .
.
综上,![]() 为定值7.
为定值7.
②当直线的斜率不存在时,由①知![]() ,
,![]() ,
,
此时![]() ;
;
当直线![]() 斜率存在时,设直线方程为
斜率存在时,设直线方程为![]() ,由①知
,由①知![]() ,
,
![]() ,
,![]() ,
,
![]()
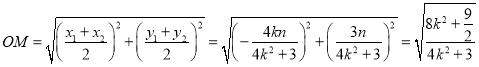 ,
,
即![]() ,
,
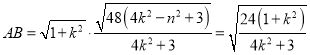 ,
,
![]()
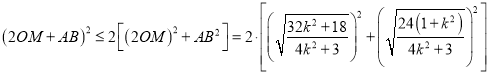
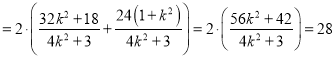 ,
,
当且仅当![]() 即
即![]() 时等号成立,
时等号成立,
![]() 当直线斜率存在时,
当直线斜率存在时,![]() .
.
又![]() ,
,
![]()
![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
【题目】某养殖场需要通过某装置对养殖车间进行恒温控制,为了解日用电量![]() 与日平均气温
与日平均气温![]() (℃)之间的关系,随机统计了某5天的用电量与当天平均气温,并制作了对照表:
(℃)之间的关系,随机统计了某5天的用电量与当天平均气温,并制作了对照表:
日平均气温(℃) | 3 | 4 | 5 | 6 | 7 |
日用电量( | 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)请利用(Ⅰ)中的线性回归方程预测日平均气温为12℃时的日用电量.
附:回归直线的斜率和截距的最小二乘法估计公式分别为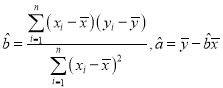 .
.