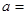题目内容
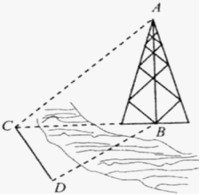
如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12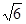 海里,在A处看灯塔已在货轮的北偏西30°,距离为8
海里,在A处看灯塔已在货轮的北偏西30°,距离为8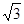 海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
(1)A处与D处之间的距离.
(2)灯塔C与D之间的距离.
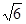 海里,在A处看灯塔已在货轮的北偏西30°,距离为8
海里,在A处看灯塔已在货轮的北偏西30°,距离为8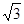 海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:(1)A处与D处之间的距离.
(2)灯塔C与D之间的距离.
(1)AD=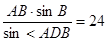 (海里);(2)
(海里);(2)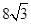 海里.
海里.
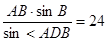 (海里);(2)
(海里);(2)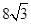 海里.
海里.(1)解△ABD,已知两角一边利用正弦定理即可.
(2)在(1)的基础上,解△ADC,已知两边及其夹角,利用余弦定理即可求解.
解:(1)△ABD中,∠ADB=60°,∠B=120°- 75°= 45° AB=12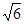
∴AD=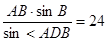 (海里) 6’
(海里) 6’
(2)△ADC中,CD2=AD2+AC2-2AD·AC·cos30°
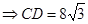 (海里) 12’
(海里) 12’
(2)在(1)的基础上,解△ADC,已知两边及其夹角,利用余弦定理即可求解.
解:(1)△ABD中,∠ADB=60°,∠B=120°- 75°= 45° AB=12
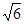
∴AD=
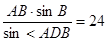 (海里) 6’
(海里) 6’(2)△ADC中,CD2=AD2+AC2-2AD·AC·cos30°
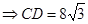 (海里) 12’
(海里) 12’
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
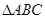 中,
中,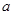 ,
,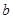 ,
,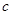 分别为内角
分别为内角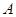 ,
,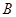 ,
,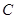 所对的边,且满足
所对的边,且满足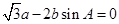 .
.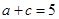 ,且
,且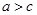 ,
,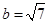 ,求
,求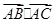 的值.
的值.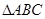 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为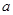 、
、 、
、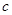 ,已知
,已知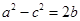 ,且
,且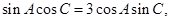 则b=____________.
则b=____________.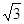 ,求边长a , b ;(2).若
,求边长a , b ;(2).若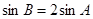 ,求ΔABC的面积.
,求ΔABC的面积.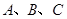 是
是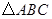 的三个内角,且满足
的三个内角,且满足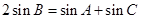 ,设
,设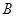 的最大值为
的最大值为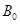 .
.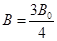 时,求
时,求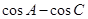 的值.
的值.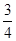 ,求b的值
,求b的值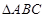 中,
中,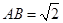 ,
,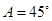 ,
,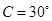 ,则
,则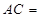
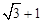
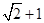
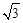
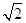
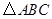 中,
中, ,
,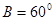 ,
,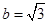 ,那么
,那么