题目内容
已知在△ABC中,角A、B、C的对边分别为a,b,c。且C=2A,a+c=10,cosA=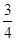 ,求b的值
,求b的值
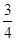 ,求b的值
,求b的值b=5
先利用正弦定理求得a=4,c=6,再利用余弦定理求得b=4或b=5,注意检验得b=5
解:∵C=2A,a+c=10,cosA=34
由正弦定理a/sinA=c/sinC可得a/sinA=(10-a)/sin2A=(10-a)/2sinAcosA
化简可得a=4,c=6……….6分
利用余弦定理可得,cosA=3/4=(b2+c2-a2)/2bc=b2+20/12b
∴b=4或b=5……….8分
当b=4时由题意可得A=B=π/4,C=(1/2)π不符合题意故舍去
故b=5……….12分
解:∵C=2A,a+c=10,cosA=34
由正弦定理a/sinA=c/sinC可得a/sinA=(10-a)/sin2A=(10-a)/2sinAcosA
化简可得a=4,c=6……….6分
利用余弦定理可得,cosA=3/4=(b2+c2-a2)/2bc=b2+20/12b
∴b=4或b=5……….8分
当b=4时由题意可得A=B=π/4,C=(1/2)π不符合题意故舍去
故b=5……….12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
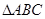 的内角
的内角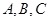 的对边分别为
的对边分别为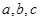 ,且
,且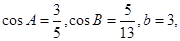 则
则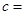
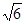 海里,在A处看灯塔已在货轮的北偏西30°,距离为8
海里,在A处看灯塔已在货轮的北偏西30°,距离为8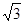 海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求: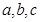 ,且
,且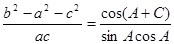
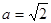 ,求
,求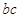 的取值范围.
的取值范围.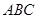 中,
中,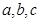 分别为内角
分别为内角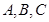 的对边,已知
的对边,已知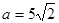 ,
,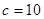 ,
,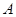 =
=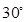 ,则角
,则角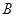 等于( )
等于( )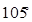
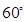
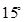
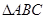 中,若sinA︰sinB︰sinC=
中,若sinA︰sinB︰sinC=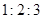 ,则
,则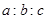 等于( )
等于( ) 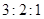
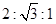

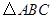 中,
中,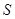 为
为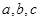 为
为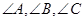 的对边,
的对边,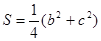 ,则
,则