题目内容
已知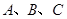 是
是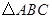 的三个内角,且满足
的三个内角,且满足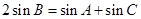 ,设
,设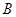 的最大值为
的最大值为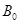 .
.
(Ⅰ)求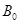 的大小;
的大小;
(Ⅱ)当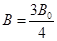 时,求
时,求 的值.
的值.
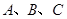 是
是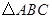 的三个内角,且满足
的三个内角,且满足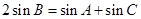 ,设
,设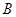 的最大值为
的最大值为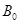 .
.(Ⅰ)求
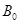 的大小;
的大小;(Ⅱ)当
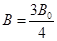 时,求
时,求 的值.
的值.(1)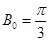 ;(2)
;(2)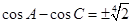 .
.
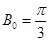 ;(2)
;(2)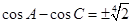 .
.本试题主要是考查了解三角形的运用。利用正弦定理和余弦定理求解三角形,以及三角恒等变换的综合运用。
解:(Ⅰ)由题设及正弦定理知,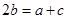 ,即
,即 .
.
由余弦定理知, ············ 2分
············ 2分
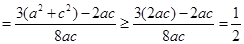 .··················· 4分
.··················· 4分
因为 在
在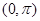 上单调递减,所以
上单调递减,所以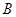 的最大值为
的最大值为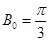 .········· 6分
.········· 6分
(Ⅱ)解:设 ,························ ①
,························ ①
······································ 8分
由(Ⅰ)及题设知 .····················· ②
.····················· ②
由①2+②2得,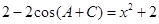 .··················· 10分
.··················· 10分
又因为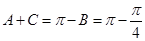 ,
,
所以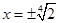 ,即
,即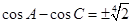 .··················· 12分
.··················· 12分
解:(Ⅰ)由题设及正弦定理知,
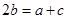 ,即
,即 .
.由余弦定理知,
 ············ 2分
············ 2分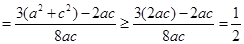 .··················· 4分
.··················· 4分因为
 在
在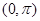 上单调递减,所以
上单调递减,所以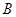 的最大值为
的最大值为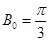 .········· 6分
.········· 6分(Ⅱ)解:设
 ,························ ①
,························ ①······································ 8分
由(Ⅰ)及题设知
 .····················· ②
.····················· ②由①2+②2得,
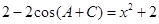 .··················· 10分
.··················· 10分又因为
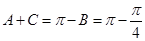 ,
,所以
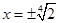 ,即
,即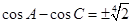 .··················· 12分
.··················· 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
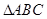 的内角
的内角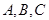 的对边分别为
的对边分别为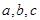 ,
,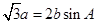 .
.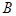 的大小;
的大小;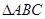 的面积等于
的面积等于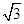 ,
,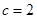 ,求
,求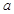 和
和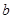 的值.
的值.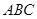 中,
中,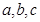 分别为内角
分别为内角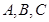 的对边,且
的对边,且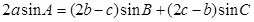 .
.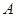 的大小;
的大小;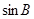 +
+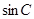 =
=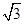 ,试判断△
,试判断△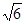 海里,在A处看灯塔已在货轮的北偏西30°,距离为8
海里,在A处看灯塔已在货轮的北偏西30°,距离为8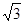 海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求: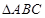 中,
中,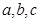 分别是角
分别是角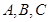 的对边,若
的对边,若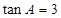 ,
,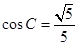 。
。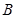 的大小;
的大小;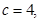 求
求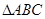 中,
中,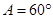 ,
,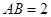 ,且
,且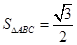 ,则边
,则边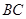 的长为( )
的长为( )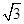
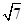
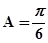 ,
,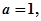 ,
,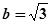 ,则c=( )
,则c=( )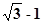 D、
D、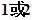
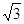 , A=30°,则B等于 ( )
, A=30°,则B等于 ( )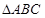 中,若
中,若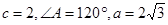 ,则
,则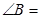 .
.