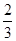题目内容
数列{an}满足a1=2,且对任意的m,n∈N*,都有 =an,则a3= ;{an}的前n项和Sn= .
=an,则a3= ;{an}的前n项和Sn= .
 =an,则a3= ;{an}的前n项和Sn= .
=an,则a3= ;{an}的前n项和Sn= . 8 2n+1-2
由 =an可得
=an可得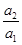 =a1,
=a1,
所以a2=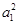 =22=4.
=22=4.
所以a3=a1a2=2×4=8.
由 =an得
=an得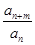 =am,
=am,
令m=1,得 =a1=2,
=a1=2,
即数列{an}是公比为2的等比数列,
所以Sn=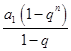 =
=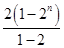 =2n+1-2.
=2n+1-2.
 =an可得
=an可得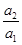 =a1,
=a1,所以a2=
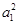 =22=4.
=22=4.所以a3=a1a2=2×4=8.
由
 =an得
=an得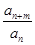 =am,
=am,令m=1,得
 =a1=2,
=a1=2,即数列{an}是公比为2的等比数列,
所以Sn=
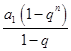 =
=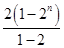 =2n+1-2.
=2n+1-2.
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 -
- +
+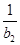 +…+
+…+ ,求T2012;
,求T2012;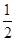 ,a3=
,a3=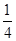 ,ak=
,ak=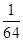 ,则k等于( )
,则k等于( )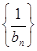 的前n项和Tn.
的前n项和Tn.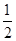 ,公比为
,公比为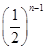


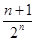
 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列,则数列
成等差数列,则数列
 等于( )
等于( )