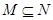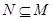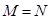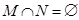题目内容
设A={x|x2-2x-8≤0}，B{x|（x-m）[x-（m-3）]≤0，（m∈R）}．
（1）若A∩B=[2，4]，求实数m的值．
（2）若A⊆∁RB，求实数m的取值范围．
（1）若A∩B=[2，4]，求实数m的值．
（2）若A⊆∁RB，求实数m的取值范围．
（1）A={x|-2≤x≤4}，B={x|m-3≤x≤m}，
∵A∩B=[2，4]，
∴
，∴m=5．
（2）A={x|-2≤x≤4}，B={x|m-3≤x≤m}，
CRB={x|x＜m-3或x＞m}，
∵A⊆CRB，
∴4＜m-3，或m＜-2，
所以m∈（-∞，-2）∪（7，+∞）．
∵A∩B=[2，4]，
∴
|
（2）A={x|-2≤x≤4}，B={x|m-3≤x≤m}，
CRB={x|x＜m-3或x＞m}，
∵A⊆CRB，
∴4＜m-3，或m＜-2，
所以m∈（-∞，-2）∪（7，+∞）．
练习册系列答案
相关题目
，使得对于
，都有
（
），则称
是M的最大（小）值.若A是一个不含零的非空实数集，且
是A的最大值，则（ ）
时，
是集合
的最小值
时，
的最小值
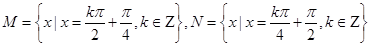,则( )
